所见即所得的数字电路教程

数字电路系统是现代计算机与电子工业工程的基础。本教程将介绍如何使用一种新兴的硬件描述语言 NetX 进行数字电路设计。在设计和实现数字电路时，我们脑海里总是会先有一个大概的电路图，接着使用硬件描述语言来描绘它——而 NetX 代码的组织形式与电路图的结构非常相似，用 NetX 编码几乎就是所见即所得地描述电路图的过程。

本教程只作简单介绍。更多细节可以参考 NetX 的语言手册。

语言概览

组合电路

我们首先介绍 NetX 中最基础的两个运算符，|| 与 <>，分别称作并行组合子（Parallel Combinator）与串行组合子（Sequential Combinator）。简单来说，|| 就像把两个电路元件并排放置，而 <> 就像用导线连接元件的输出和输入。

下面我们小试牛刀，用这两个运算符把两个 2-1 与门组合成一个 4-1 与门：

我们从一个 2-1 与门 AND 出发，首先用 || 并列连接两个与门，这就得到了一个 4-2 的特殊电路元件。这个元件的内部有两个并列的与门，分别处理整个元件的前两个、后两个输入并分别输出。接下来，我们用 <> 将这个元件的输出串接到第三个 2-1 与门上，也就得到了一个 4-1 的电路元件——也就是一个 4-1 与门。

使用 NetX 内置的、包括 AND 的各种基础逻辑门，我们还可以组合出稍复杂一些的元件。

比如，可以通过下面的代码实现一个半加器。半加器是一种基本的数字电路元件，它实现了两个 1-bit 二进制数的加法。不过要注意，1-bit 二进制数只能是 0 或 1，而他们的和 2 需要 2-bit 才能表示（表示为 10）。这里，我们把两个输入 1-bit 二进制数记作 a 和 b，对于他们的 2-bit 和，我们将高位记作 carry（进位），低为记作 sum（和）。具体来说，半加器的逻辑关系如下表所示：

a	b	carry	sum
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

仔细观察，我们发现 carry 实际上可以由一个与门得到，而 sum 可以由一个异或门得到：

component HA : [a, b] -> [sum, carry] {
	wire a, b, sum, carry of bit(1);
	  sum <> XOR <> (a || b); 
	carry <> AND <> (a || b);
}

这里，语句 wire a, b, sum, carry of bit(1); 定义了四个 1-bit 的“电线”元件。电线可以理解为一种特殊的 1-1 元件，它会直接将得到的输入传递到输出端口。如果一个电线的名字（比如 a）在代码中出现了多次，我们会认为他们是同一根电线。比如在上面的代码中，a 和 b 分别出现了两次，代表着与门和异或门的输入是相同的电线。

上述代码刻画的电路图如下所示：

add

半加器实现了 1-bit 二进制数的加法，接着我们来实现 4-bit 甚至更复杂的二进制加法。假设我们现在有 4-bit 宽的输入 a 和 b，要输出 4-bit 和 c。

最简单的思路是从低位向高位依次计算每一个二进制位的和，并将可能产生的进位向后传递。这里“每一个二进制位的和”可以用刚刚实现的半加器来实现。

我们用 a[i] 表示输入 a 的第 i 位。注意：在计算每一位二进制的和时，除了要考虑当前的输入 a[i] 和 b[i]，我们还需要考虑前一位加法进位 cin。而半加器只能处理两个输入，我们还需要实现一个能将三个 1-bit 二进制数加起来的元件——也就是全加器。

在实现全加器之前，我们先来了解一个特殊的内置元件 TO，它可以理解为匿名的”电线”。一般有名字的电线多次出现时，NetX 会认为他们总是同一根电线；但是 TO 多次出现时，它们总是不同的电线。

利用 TO，我们可以用下面的方式，十分简洁地实现一个全加器：

let FA = (TO || OR) <> (HA || TO) <> (TO || HA);

这行代码乍看之下让人有些摸不着头脑——但结合图片左上角的全加器电路图来看，就清楚多了。

全加器是将两个半加器前后组合起来实现 3-bit 加法的元件，而上面的代码就描述了这种“前后组合”的图形模式：

面对三个输入信号，我们将其中一个留空，将另外两个传入半加器 FA
让刚刚留空的信号也参与到加法中：将它与 FA 的 sum 位通过另一个 FA 相加
此时，两个 FA 的进位位 carry 还没有处理。由于三个 1-bit 加法的性质，这两个 carry 只可能有一个为 1，因此我们可以用一个或门 OR 将它们的输出相加，得到最终的进位输出。

当然，这样的写法有些抽象，刚刚接触 NetX 语言难免会有些不适应。

我们也可以用更传统的方式，给每个元件的输入输出端口起个名字，写成下面的样子：

component FA : [a, b, cin] -> [sum, cout] {
    wire a, b, cin, sum, cout of bit(1);
    wire tmp_sum, c1, c2 of bit(1);
    (tmp_sum || c1) <> HA <> (b || cin);
        (sum || c2) <> HA <> (a || tmp_sum);
    cout <> OR <> (c1 || c2);
}

实现了全加器，只需要把他们的进位串联起来，就能实现 4-bit 甚至更复杂的二进制加法了。

我们考虑第 i 个全加器，它需要将 a[i] 和 b[i] 相加，把结果传递给 c[i]，把进位传递给第 i+1 个全加器。我们用 pattern(i) 表示这种连线的模式：

let pattern(i) =
	(#c[i] || TO) <> FA <> (a[i]# || b[i]# || TO);

这里，我们将 a[i], b[i], c[i] 绑定到全加器的端口上，并且把进位输入和输出留空，之后再处理。

这里出现了一个新的运算符 #，它叫作端口装饰器（Port Decorator），可以用来“堵住”某个元件的输入输入端口。比如

#c[i] 表示只使用 c[i] 的输入端口，堵住它的输出端口
a[i]# 表示只使用 a[i] 的输出端口，堵住它的输入端口

在全加器的这种连线模式中， a[i] 和 b[i] 是整个模块的输入，它们的输入端口应该留空以待后续使用。我们不希望他们在加法器模块里就被占用，干脆用一个 # 把端口堵上，让其他元件没法与他们相连。对于 c[i] 也是类似，只不过我们堵上的是它的输出端口。

好了，这样我们定义了 pattern(i)，它是一种新的 1-1 的元件，接受进位输入 cin，输出新的进位 cout。把初始进位设置为 1-bit 的 0，然后把 pattern(i) 首尾相连，也就得到了我们想要的 4-bit 加法器：

component ADDER : [a, b] -> [c] {
	wire a, b, c of bit(4);
	let FA = /* ... */;
	let pattern(i) = /* ... */;
	let adder(i) =
		if i < 0 then 1'b0
		else pattern(i) <> adder(i - 1);
	adder(3);
}

这里我们用到了递归的写法。adder(3) 会被一步展开成

pattern(3) <> adder(2)

接着一步步变成

pattern(3) <> pattern(2) <> pattern(1) <> pattern(0) <> 1'b0

从而实现了这个 4-bit 的加法器。

当然，如果你不熟悉递归的写法，也可以引入一个中间变量，写成下面的样子：

component ADDER : [a, b] -> [c] {
	wire a, b, c of bit(4);
	wire carry of bit(4);
	let cin(i) = if i == 0 then 1'b0 else carry[i - 1];
	for (i in [0..4]) {
		(c[i] || carry[i]) <> FA <> (
			a[i] || b[i] || cin(i)
		);	
	}
}

下面我们考虑另外一种常见的组合电路：编码器（Encoder），我们常常用它将热独码转为二进制码。

热独码（One-hot code）指的是考虑有 \(2^n\) 个 bit 的输入，其中只有一个 bit 为 1，其余的都为 0。假设其中第 i 个 bit 为 1，那么编码器就是要输出 i 的 n-bit 二进制表示。

下面展示了一个 4-2 编码器的电路图：

encoder

编码器的电路图乍看之下有些复杂，但仔细观察也能发现其中的规律：既然只有一个输入为 1，那么让这一位信号传递到应该为 1 的输出端口就可以了。而

假设输入的第 i 位为 1
第 j 个输出端口输出的是 i 的二进制表示的第 j 位

也就是说，如果 i 的第 j 位为 1（换言之，(i >> j) & 1 == 1），那么第 j 个输出就会和第 i 个输入相连。我们可以用下面的代码来表达这种模式：

component ENCODER(n) : [input] -> [output] {
	let power = 2 ** n;
	wire input of bit(power);
	wire output of bit(n);
	for (j in [0..n]) {
		output[j] <> OR <> [
			input[i] | i in [0..power], 
			           when (i >> j) & 1 == 1
		];
	}
}

我们定义了一个编码器模块 ENCODER，它含有一个属性 n 指示：输入的编码有 \(2^n\) 位，输出的编码有 \(n\) 位；我们依照这个规约定义 input 和 output。

接着来考虑每个输出位 output[j] 的来源。这里出现了一种新的表达式：列表推导（List Comprehension）。

列表在 NetX 可以作为一种语法糖。列表 [e1, e2, ..., en] 也就表示 (e1 || e2 || ... || en) 这样许多个电路元件并列组合在一起的意思。只是这样看，列表和原来的写法好像也没有什么差别。但是列表还支持下面的写法：

[expr | qualifier_1, ..., qualifier_n]

这代表着根据后面列出的 qualifier 生成一个新的列表。比如，

[i**2 | i in [0..6], when i % 2 == 1]

就生成了 [1, 9, 25] 这样一个列表。这里的 i in [0..6] 表示 i 在 \(0\) 到 \(6\) 之间取值，而 when i % 2 == 1 则表示只有当 i 是奇数时才会把 i**2 加入到列表中。

具体地，在上面的编码器代码中，列表推导

[input[i] | i in [0..power], when (i >> j) & 1 == 1]

在 n = 2 即 power = 4 时，

如固定 j = 0，则得到 [input[1], input[3]]，也就是 (input[1] || input[3])，这是第 0 位输出的来源；
如固定 j = 1，则得到 [input[2], input[3]]，也就是 (input[2] || input[3])，这是第 1 位输出的来源。

通过类似的列表推导，我们就可以描述电路中复杂的连接模式，从而像上面那样简洁地实现一个编码器。

时序电路

到目前为止，我们已经大概了解了怎么使用 NetX 设计组合电路。接下来我们看看如何设计时序电路，也就是含有寄存器等存储元件，可以记录状态的电路。

NetX 内置了一个简单的寄存器 REGISTER，使用时大概像是这样：

output <> REGISTER(pos_edge = true) <> [clk, input];

寄存器有两个输入信号，记作 clk 和 input。其中 clk 是时钟信号：

如果寄存器是上升沿触发的（pos_edge = true），那么当 clk 从 0 变为 1 时，寄存器才会把当前 input 的值存储下来。
如果寄存器是下降沿触发的（pos_edge = false），那么当 clk 从 1 变为 0 时，寄存器才会把当前 input 的值存储下来。

寄存器的输出信号 output 就是当前寄存器内部存储的值。

在实际应用中，我们经常需要包含复位信号的寄存器。

复位信号可以在系统启动或出错时将寄存器强制设置为已知的初始值：

import std.selector.MUX; // 从标准库里引入多路选择器 MUX

/**
  * Register component
  *
  * This component implements a register with synchronous reset.
  *
  * @attr pos_edge   Triggers on rising edge of clock when true
  * @attr high_rst   Enables active-high reset when true
  * @attr rst_value  Value to load on reset
  *
  * @port clk        Clock signal
  * @port rst        Reset signal
  * @port input      Input data to be registered
  * @port output     Output data from the register
  */
component REG(pos_edge, high_rst, rst_value) : [clk, rst, input] -> [output] {
	wire clk of clock(); // 声明为时钟信号，也可以直接写成 wire clk of clock;
	auto input, output;  // 让编译器根据使用场景自动推断位宽
	
	output <> REGISTER(pos_edge) <> [
		clk, MUX(1) <> (
			if high_rst 
			then [rst, input, rst_value]
			else [rst, rst_value, input]
		)
	];
}

这里 MUX 是数字电路中的条件选择模块，我们已经在 NetX 的标准库里实现了一份。

MUX(1) 元件有三个输入，sel, input_0 和 input_1。这里传入的属性 1 代表了选择信号 sel 的宽度：1-bit 的选择信号可以在两个分支输入中选择一个输出：

若 sel = 0，则选择器输出 input[0] 的值
若 sel = 1，则选择器输出 input[1] 的值

特别地，在我们的复位寄存器中，MUX(1) 的参数顺序会依据 high_rst 的值修改：

当 high_rst = true 时，意味着当 rst 信号为 1 时重置寄存器的值，于是 MUX 的参数顺序应当为 [rst, input, rst_value]
当 high_rst = false 时，意味着当 rst 信号为 0 时重置寄存器的值，于是 MUX 的参数顺序应当为 [rst, rst_value, input]

在使用这个含有复位信号的寄存器时，我们就可以写成：

my_output <> REG(true, true, 0) <> [my_clk, my_rst, my_input]

或者为了让代码更清晰，也可以显式地指定属性、输入、输出的名字，写成：

{output : my_output} <> REG (
	pos_edge = true, 
	high_rst = true, 
	rst_value = 0
) <> {
	clk : my_clk,
	rst : my_rst,
	input : my_input
};

这种写法可以看清每个信号的用途，在复杂的电路中会特别有用。

现在我们就可以利用寄存器设计时序电路了。

我们先来看一个经典的例子：用时序电路实现一个简单的红绿灯状态机。

它有红绿黄三种状态，红灯亮 30 秒时将会变为绿灯，绿灯亮 25 秒后变为黄灯，黄灯亮 5 秒后变为红灯。我们可以用一个状态转移图来描述这个过程：

traffic

假设我们已经有了一个周期为一秒的时钟信号；对照状态转移图，我们可以设计出下面的电路：

import std.utils.REG;

// 定义枚举类型，包含红绿黄三种状态
// 编译器会自动推断 State 的位宽为 2
// 并且分配 RED=2'b00, GREEN=2'b01, YELLOW=2'b10
enum State {
  RED, GREEN, YELLOW
};

// 计数器组件，用来记录距离上次变灯经过的时间
component COUNTER : [clk, rst] -> [count] {
	wire count of bit(32);
	wire clk of clock();
	wire rst of bit(1);
	
	// 当 rst 信号到来时重置为 0，否则每个时钟周期加 1
	count <> REG (
		pos_edge=true, high_rst=true, rst_value=0
		) <> [clk, rst, ADD <> [count, 1]];
}

// 红绿灯状态机组件
component TRAFFIC_LIGHT : [clk] -> [color] {
	wire color of State;   // 定义当前颜色 color，位宽为 2
	wire clk of clock();
	
	wire change of bit(1);	// 判断是否需要变灯
	auto counter <> COUNTER <> [clk, change];	// 变灯时需要重置计数器
	change <> EQ <> [	// 如果计数器的值等于当前颜色对应的阈值，则需要变灯
		counter,
			MUX(2) <> {	// 根据当前颜色，决定变灯时的计数器阈值
			sel          : color, 
			case[RED]    : 30, 
			case[GREEN]  : 25, 
			case[YELLOW] : 5, 
			$default     : 0
		}
	];
	
	let clocked_reg = REGISTER(pos_edge = true) <> [TO, clk#]; 
	color <> clocked_reg <> MUX(1) <> [change,	// 用于保存当前颜色状态的寄存器
		color,	// 如果无需变灯，保持当前颜色
		MUX(2) <> {	// 否则，根据当前颜色决定下一个颜色
			sel          : color, 
			case[RED]    : GREEN, 
			case[GREEN]  : YELLOW, 
			case[YELLOW] : GREEN, 
			$default     : RED
		}
	];
}

注意，这里 MUX 又用到了按名字连接的语法。这里的表达式

MUX(2) <> {	// 根据当前颜色，决定变灯时的计数器阈值
	sel          : color, 
	case[RED]    : 30, 
	case[GREEN]  : 25, 
	case[YELLOW] : 5, 
	$default     : 0
}

实际上等价于 MUX(2) <> [color, 30, 25, 5, 0]，几个输入分别对应 MUX(2) 模块的输入端口 [sel, case[0], case[1], case[2], case[3]]。使用按名连接的方式让代码变得更清晰了。

NetX 的设计的特点在于“所见即所得”：

就算你不理解电路背后的原理，只要从电路图出发一笔一画地临摹，就能将电路实现出来。

这里我们借用 ICCD’96 的一篇论文提出的开平方电路作为例子。文章中给出了这样一个设计，它每个周期处理两位输入信号，用总计 16 个时钟周期计算 32 位数的平方根。

电路图如下所示：

sqrt

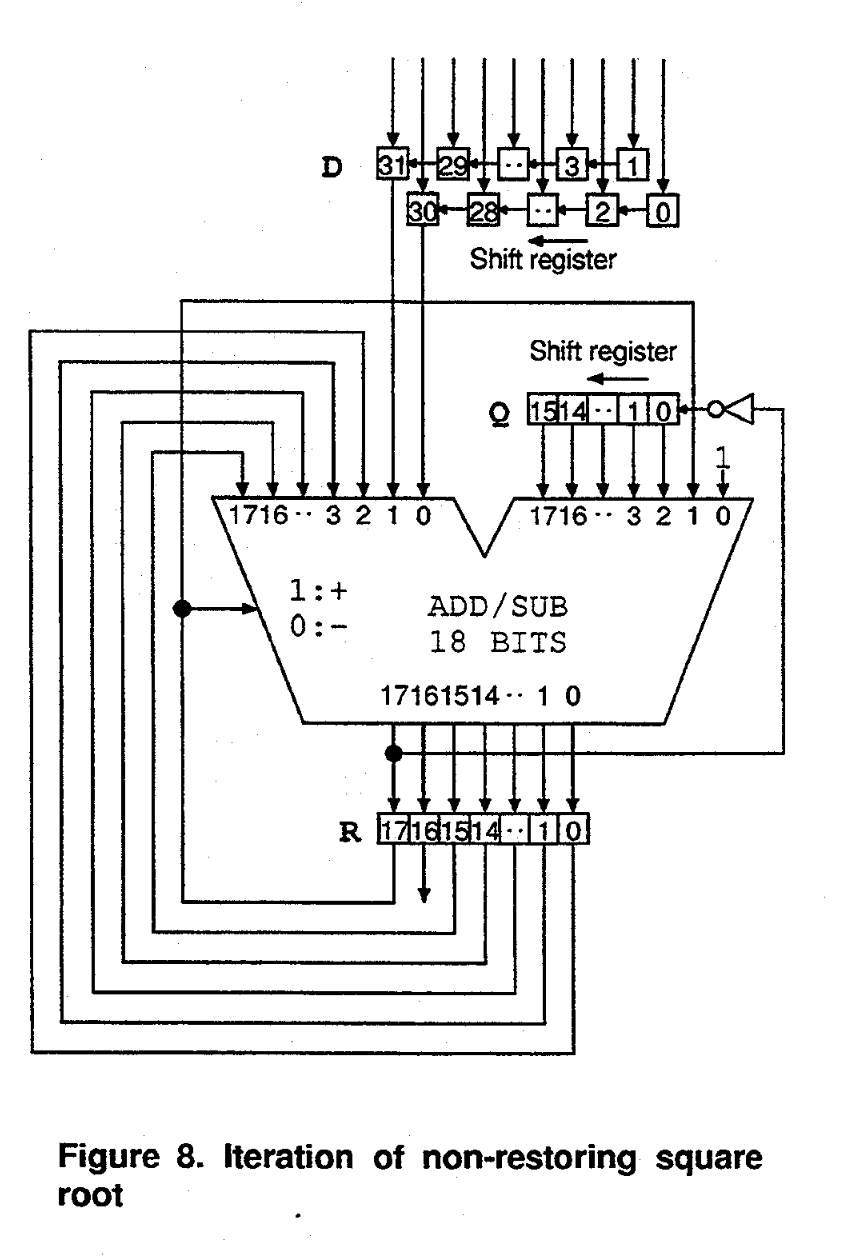
即便你没有读过这篇论文、也完全不理解这个开方算法的原理，还是可以用 NetX 绘制这个电路图；之后就可以通过 NetX 的编译器、仿真器等设施真正地实现这个电路。

下面是这个开平方电路的 NetX 代码实现，注意观察代码中的各个元件和电路图的对应关系：

import std.memory.SHIFT_REG; // 从标准库引入移位寄存器 SHIFT_REG
import std.utils.REG;

component SQRT32(pos_edge, high_rst) : [clk, rst, D] -> [Q] {
  wire clk of clock();
  wire rst of bit(1);
  wire D of bit(32);
  wire Q of bit(16);

  wire R, R_next, lhs, rhs of bit(18);
  let shift(init_value) = SHIFT_REG(16, pos_edge, high_rst, init_value) <> [clk#, rst#, TO];
  
  // 这里 CONCAT 是一种内置组件，它将所有输入信号前后连接成一个更宽的信号
  auto D_odd <> shift(CONCAT <> [D[i * 2 + 1] | i in [16..0]]) <> 1'b0;
  auto D_eve <> shift(CONCAT <> [D[i * 2]     | i in [16..0]]) <> 1'b0;
  Q <> shift(16'd0) <> NOT <> R_next[17];

  lhs <> CONCAT <> [R[15:0], D_odd[15], D_eve[15]];
  rhs <> CONCAT <> [Q, R[17], 1'b1];
  R_next <> MUX(1) <> [
    R[17],
    SUB <> [lhs, rhs],
    ADD <> [lhs, rhs]
  ];
  R <> REG(pos_edge, high_rst, 18'd0) <> [
    clk, rst, R_next
  ];
}

可以发现，电路图中的每一个组件（框图）、每一条线网（连线），在 NetX 代码中均有明确的对应。比如电路图中将输入信号 D 分成两部分，分别传入了一个移位寄存器；在代码中也就有 D_odd 和 D_eve 与之对应。

工具链使用

上文中，我们大致了解了如何用 NetX 语言设计电路。下面我们将介绍 NetX 目前的工具链，如何用这些工具编译、仿真、测试 NetX 程序，并将它们部署到 FPGA 上。

这里我们以项目 NetX-RISC-V 为例，介绍这一过程。

该项目实现了一个单周期的 RISC-V 处理器。该处理器实现了除 FENCE 以外的所有 RV32I 指令。
它可以被部署在一块 Terasic DE2-115 FPGA 开发版上，并使用其板载存储作为指令、数据存储器。
它可以使用 C++ 编写的 testbench 进行仿真测试。该 testbench 使用：
- RISC-V 官方测试集中的指令单元测试程序作为激励
- C++ 实现的软件模拟板载存储器

具体电路图与实现可以点击上面的链接查看，这里我们主要介绍工具链的使用。

编译与包管理

NetX-RISC-V 项目中包含了一个配置文件 _netx.toml 如下：

[project]
name = "rv32i"
version = "0.1.0"
include = [ "rv32i.nx" ]

[dependencies]
std = { version = "0.1.0", git = "git@github.com:pascal-lab/NetX-std.git" }

它声明了该项目的名称、版本号、包含的源文件。特别地，该项目只包含一个单文件 rv32i.nx。此外，该文件包含了一个依赖项 std，并指定了 git 仓库地址。

包管理器会自动解析配置文件，分析依赖项（如果是非本地的依赖，会自动下载）并进行编译。

这里，可以使用下面的指令进行编译。

nx compile _netx.toml --top CORE --output out.json

编译会产生一个 JSON 文件 out.json，它是硬件图的底层表示。

关于更多的编译选项与配置，参见 NetX 仓库。

Nxon 底层表示

Nxon 是基于 JSON 的硬件图底层表示，它是 NetX 编译器的标准输出格式。Nxon 文件主要包含个元件的实例化以及端口连接情况。下面展示了处理器的 Nxon 表示，其中许多地方有省略：

{
  "totalData": 1063,
  "top_input": ["clk", "rst", "instr", "dmem_out"],
  "top_output": ["imem_addr", "dmem_addr", "dmem_in", "dmem_op", "dmem_wr"],
  "design": {
    "type": "component",
    "id": "CORE",
    "loc": "rv32i.nx:7:10",
    "input": ["clk@0", "rst@1", "instr@2", "dmem_out@3"],
    "output": ["imem_addr@4", "result@5", "Rb@6", "ctl.mem_op@7", "ctl.mem_wr@8"],
    "members": [
      {"type": "clock", "id": "clk@0", "loc": "rv32i.nx:8:9"},
      {"type": "wire", "width": 1, "id": "rst@1", "loc": "rv32i.nx:9:9"},
      {"type": "wire", "width": 32, "id": "instr@2", "loc": "rv32i.nx:10:9"},
      ...
      {"type": "component", "id": "INSTR_DECODER", ... },
      {"type": "component", "id": "IMM_SELECTOR", ... },
      {
        "type": "component", "id": "REG_FILE", "loc": "19:10",
        "input": [ ... ],
        "output": [ ... ],
        "attribute": {"high_rst": "true", ...},
        "members": [
          {"type": "component", "id": "DECODER", ... },
          {"type": "component", "id": "MUX", ... },
          {"type": "builtin", "id": "AND", ... },
          ...
        ]
      }
      ...
    ]
  }
}

这一表示说明了顶层元件为 CORE，它内部包含了指令译码器 INSTR_DECODER，立即数选择器 IMM_SELECTOR，寄存器堆 REG_FILE 等元件。其中每个元件又包含了各自的子元件。

元件含有下面的属性：

type：JSON 对象的类型。对于用户定义的元件，该项设置为 component
id：该元件在定义时的唯一标识符
loc：该元件定义的源码位置，格式为 文件名:行号:列号。如 "loc" : "rv32i.nx:7:10" 表示该元件的定义在源代码文件 rv32i.nx 的第 7 行第 10 列。
input 和 output：指示该元件的输入输出线。
members：该元件的内部结构。可能包括线网的定义，或者包含其他的元件。

特别需要注意是这里的线网定义（如 clk@0，rst@1）。这里，@ 符号之前的字符串是他们在源码中的名字，而 @ 符号之后的数字是它们在 Nxon 中的唯一标识符。由于在 Nxon 表示中消去了源码中的作用域信息，可能会出现重名的情况，因此需要用唯一标识符来区分。

关于 Nxon 表示的详细说明，参见 NetX 标准手册。

仿真测试

NetX 提供了 C++ 实现的仿真库 nxsim，可以用它来对 Nxon 文件进行仿真测试。

下面展示了项目中 main.cpp 的部分内容，该文件提供了仿真所需的测试激励

#include <nxsim/circuit.h>
#include <nxsim/circuit_parser.h>

class Memory {
    /*...*/
};

int main() {
    std::string json;
    std::getline(std::cin, json);
    auto ctx = nxon::parse_circuit(nlohmann::json::parse(json));
    /*...*/
    for (/*...*/) {
        const auto instr_mem = new Memory(/*...*/);
        const auto data_mem = new Memory(/*...*/);
        ctx.update_by_name("rst", value_t{1, 1});
        ctx.flip_by_name("clk");
        /*...*/
        if (/*...*/) {
            if (static_cast<unsigned>(ctx.get_by_name("data[10]")) == 0x00c0ffee) {
                std::cout << "\t-> \033[32mPassed!\033[0m" << std::endl;
                passed++;
            } else {
                std::cout << "\t-> \033[31mFailed!\033[0m" << std::endl;
            }
            break;
        }
    }
}

可见，这里

我们从标准输入读取 Nxon 文件的内容，并解析为一个电路上下文 ctx。
对于每个测试用例，我们创建了两个内存对象 instr_mem 和 data_mem，分别模拟指令存储器和数据存储器。
我们通过 ctx.get_by_name， ctx.update_by_name 以及 ctx.flip_by_name 等方法访存当前电路状态。注意，仿真器只允许对顶层模块的输入信号进行修改，但可以对任意电路中的信号进行读取。

如遇到重名等问题难以直接访问时，可以参照 Nxon 文件，通过 ctx.circuit.get_value(417) 的方式，通过 Nxon 中的唯一标识符获取电路状态。

除此之外，仿真器还支持导出波形图、检测用例覆盖率等功能。细节见 NetX 仓库中提供的文档。

编写了 C++ 测试激励之后，就可以使用下面的命令编译并运行测试：

c++ -O3 -ffast-math -std=c++23 -flto -o risc_test main.cpp -lnxsim

这里

-O3 -ffast-math 是编译器的优化选项，开启了高级别的优化以保证仿真速度
-std=c++23 指定了 C++ 的标准版本
-flto 开启了链接时优化选项。由于 nxsim 被编译为一个静态链接库，开启该选项可以让编译器在链接时根据当前测试激励编写情况作进一步的优化。
-lnxsim 指定了链接时需要链接的库，即 nxsim 仿真库。

此时，将编译出的项目 Nxon 文件输入可执行文件 risc_test 即可。比如可以通过管道

nx compile _netx.toml --top CORE --minimal | ./risc_test

进行仿真测试。下面展示了运行的输出

Running test case: "sra.hex"    -> Passed!
Running test case: "slti.hex"   -> Passed!
Running test case: "bne.hex"    -> Passed!
Running test case: "bgeu.hex"   -> Passed!
Running test case: "lhu.hex"    -> Passed!
Running test case: "lbu.hex"    -> Passed!
Running test case: "lw.hex"     -> Passed!
Running test case: "sltu.hex"   -> Passed!
Running test case: "lb.hex"     -> Passed!
Running test case: "srli.hex"   -> Passed!
Running test case: "beq.hex"    -> Passed!
Running test case: "jal.hex"    -> Passed!
Running test case: "sw.hex"     -> Passed!
Running test case: "xori.hex"   -> Passed!
Running test case: "addi.hex"   -> Passed!
Running test case: "lui.hex"    -> Passed!
Running test case: "blt.hex"    -> Passed!
Running test case: "lh.hex"     -> Passed!
Running test case: "srl.hex"    -> Passed!
Running test case: "slli.hex"   -> Passed!
Running test case: "simple.hex" -> Passed!
Running test case: "slt.hex"    -> Passed!
Running test case: "ori.hex"    -> Passed!
Running test case: "bltu.hex"   -> Passed!
Running test case: "add.hex"    -> Passed!
Running test case: "xor.hex"    -> Passed!
Running test case: "sh.hex"     -> Passed!
Running test case: "and.hex"    -> Passed!
Running test case: "andi.hex"   -> Passed!
Running test case: "sub.hex"    -> Passed!
Running test case: "sltiu.hex"  -> Passed!
Running test case: "srai.hex"   -> Passed!
Running test case: "or.hex"     -> Passed!
Running test case: "bge.hex"    -> Passed!
Running test case: "auipc.hex"  -> Passed!
Running test case: "jalr.hex"   -> Passed!
Running test case: "sb.hex"     -> Passed!
Running test case: "sll.hex"    -> Passed!
Passed 38/38 test cases
Elapsed time: 1.42926s

电路可视化

NetX 还提供了一个可视化工具，它接受编译产生的 Nxon 文件，并且生成电路的图形化表示。

目前，可视化工具基于 Graphviz 实现，使用下面的命令生成电路图：

nx visualize _netx.toml --top CORE -o vis.dot --depth=2
dot -T pdf vis.dot -o vis.pdf

这里 --depth=2 规定了电路图展开的深度，我们从顶层元件 CORE 出发只展开两层，得到：

cpu_view

从图上依稀可以分辨出：整个图片最左侧比较杂乱的部分是指令译码器；右侧排线整齐的部分是寄存器堆；其余部分则是 ALU、立即数选择器等元件。不过，现在导出的电路图还有很大的改进空间：我们使用的 Graphviz 布局引擎不能很好地处理元件较多的电路，我们正在积极寻找改进方案。

FPGA 部署

在完成了上面的仿真测试后，我们就可以将设计部署到 FPGA 上了。

这里我们采用了一块 Terasic DE2-115 开发版，它需要与官方提供的 System Builder 与 Intel Quartus Prime 软件配合使用。

首先使用 System Builder 生成空的 Verilog 项目，该项目只包含了与 FPGA 板载资源交互的相关接口。
再使用 Intel Quartus Prime 创建与板载内存相关的 IP 核接口。

在完成上述准备后，我们只需将这些生成的接口与 NetX 设计相连即可。

使用下面的编译指令

nx dump _netx.toml --top CORE --output core.v

将 NetX 源码首先编译到 Nxon 底层表示，之后将底层表示翻译到 Verilog。注意，这里的 Verilog 表示已接近网表级表示，避开了原生 Verilog 中的各种行为级建模，仅仅保留了 always @(posedge clk) 结构表示时序逻辑和 assign lhs = rhs 表示组合逻辑。

相连得到

/*...*/
wire clk, rst;
wire [31:0] imem_out, dmem_out, dmem_in;
wire [31:0] imem_addr, dmem_addr;
wire [3:0] dmem_op;
wire dmem_we;
assign rst = SW[0];
  
mod_0 core(
    clk, rst, imem_out, 
    dmem_out, imem_addr, dmem_addr, dmem_in, dmem_op, dmem_we,
    HEX0, HEX1, HEX2, HEX3, HEX4, HEX5, HEX6, HEX7
);
  
assign LEDR = imem_addr[17:0];
    
ram_a data_mem(
	.byteena_a(dmem_op),
	.data(dmem_in),
	.rdaddress(dmem_addr[16:2]),
	.rdclock(clk),
	.wraddress(dmem_addr[16:2]),
	.wrclock(~clk),
	.wren(dmem_we),
	.q(dmem_out)
);
  
ram_b instr_mem(
	.address(imem_addr[16:2]),
	.clock(~clk),
	.data(32'b0),
	.wren(1'b0),
	.q(imem_out)
);
/*...*/

完成上述代码准备后，使用 Quartus 综合并将电路烧录到 FPGA 开发版上。
最后，使用 Quartus 的板载内存编辑器，将测试用例写入板载内存，即可进行测试。

下面展示了该项目成功执行测试程序，将 0x00C0FFEE 写入 x10 寄存器，标志测试通过的图片（为方便展示，这里还包括了 CPU 设计以外的七段数码管等）：