寻找逻各斯：语言与逻辑入门

或许源头相同的事物身上总会留存下它们共同祖先的痕迹。

或许令人有些意外：从闽南语、客家话到西北官话、东北方言，各个地方、许多的汉语方言里都有「旮旯」这个词。为什么呢？我们有许多可信的证据认为，「旮旯」和「角落」两个叠韵词实际上都是上古汉语中「角」字（音 kroog）的复辅音分拆——上古汉语当然地就是各地方言的那个共同祖先了。生物学的同源研究里也有类似的结论。比如人类和蝙蝠的前肢也有这样的相似性，暗示着我们与蝙蝠可能有一个共同的哺乳动物祖先。

我们又知道：现代语义分析中的「谓语」实际上就来自弗雷格逻辑学里的「谓词」这个术语；再向前追溯「话语」和「理性」两个意思，在古希腊竟然都可以用一个词表达——语言和逻辑里许多的相似之处，是否也暗示了它们来自一个共同的祖先、古希腊语中的这个逻各斯(λόγος) ？

我想，如果真的存在这个共同的祖先，它一定就是人类心智中最本质的那部分。既然这样，那么语言学与逻辑学的研究或许也就自然地可以指向一个终极的问题：我们是谁？我们自我意识的觉醒，究竟意味着什么？

很遗憾，这篇文章并不能回答这样的问题。不过我们将简单地了解语言学和逻辑学研究中的一些概念，并发现这些研究在方法学上的相似性，用盲人摸象的方式感受逻各斯的边界。此外，我们还将讨论一些程序设计语言理论(Programming language theory, PLT) 的结论和方法。PLT 是语言学和逻辑学共同的后代，而其中像 Curry-Howard Isomorphism 这样精巧的结论更给我们带来了一些信心——那个终极答案就在这条航线尽头的信心。

Compositional Semantics

让我们从真值条件语义学(Truth conditional semantics) 说起。所谓真值条件语义，也就是关心一个自然语言的句子的意义（语义）在何种条件下是真的。

比如你迫切地想知道传言

Alice kissed Bob at the dance party.

是否为真。语言学家可能会给出这样的分析：

首先我们试图通过分析句法范畴，画出一棵可以表示句子中的词汇之间层级结构的树：

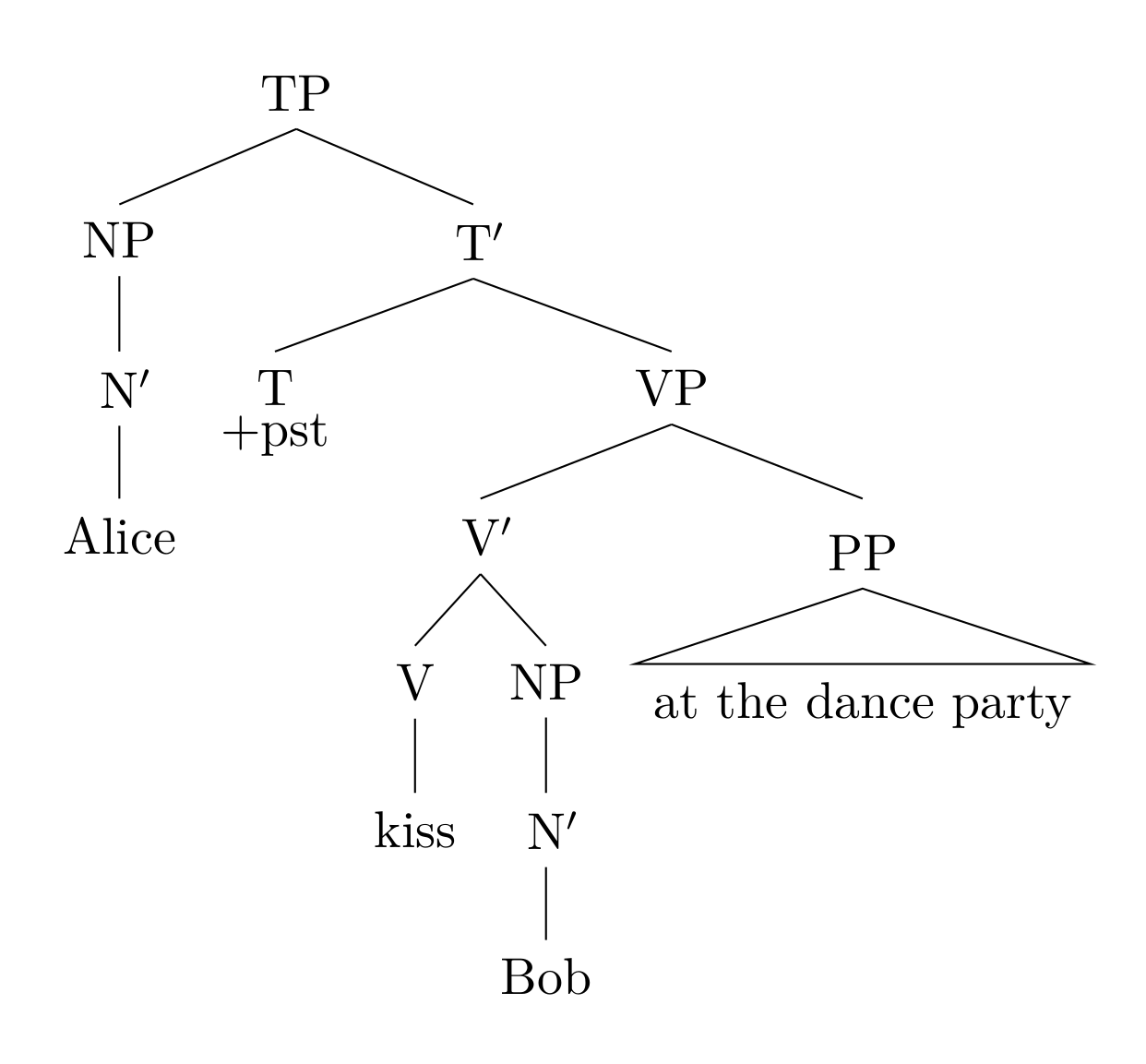
我们暂时不具体介绍句法学的理论，只给出一个简单的解释。

• 这一句子本身构成了一个 TP(Tense Phrase)，它的结构核心将句子标记成了过去时态；

• 句子的主语 Alice 本身构成了一个 NP(Noun Phrase)；

• 谓语 VP(Verb Phrase) 的结构核心即动作 kiss，它的宾语是 Bob。这个动作同时受 PP(Preposition Phrase) 的约束。

如果我们要根据这棵树的结构分析句子的语义，继而判断其真假，就需要用到真值条件语义学的方法了。所谓真值条件语义学也被称为组合语义学(Compositional Semantics)。其核心观点是相信一棵特定句法树的语义，是可以通过其子树的语义计算得到的。这种性质在语义学、逻辑学里都叫做组合性(Compositionality)。

比如对于这样的句法树：

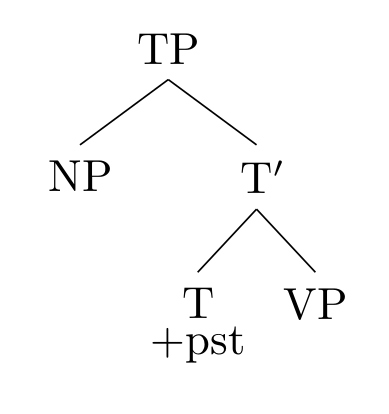
它对应的句子为真的条件是：考虑使得 VP 为真的集合，如果 NP 指称的对象在这个集合里，句子就为真，否则为假。试着把这个规则应用到我们的例子上：对于 Alice kissed Bob at the dance party 这句话，它的语义就是：考虑所有「在舞会上亲吻了 Bob 的人」构成的集合 ，如果「Alice」在这一集合中，则该句为真，否则为假。

当然，「在舞会上亲吻了 Bob 的人」的集合，又是从 VP 子结构的语义计算得到的：

在例句中，VP 有 V' 和 PP 两个子结构；

• 其中 V’ 有一个动词 kiss 和宾语 Bob 构成。

  先考虑 kiss 的真值条件。要使得 kiss 这件事确实发生，我们就考虑世界上所有已经发生过的「在丙地点，甲君亲吻了乙君」这样的事实。所有这样的甲、乙、丙都可以使得 kiss 为真，于是他们就构成了 kiss 的真值集合。

  那么如果我们在 kiss 的真值集合中删去「乙」不是 Bob 的元素，剩余元素构成的集合自然就成了 V’ 的真值集合。也就是「在某处，某人亲吻了 Bob」这样的事实组成的集合。

• 其中 PP 的内部结构被我们省略了。但我们大概可以类推出使它为真的集合应该是「所有在舞会上发生的事实」。

至此，我们得到了 VP 的两个子结构的语义，于是也就可以组合出 VP 的语义了。又要让「在某处，某人亲吻了 Bob」为真，也要「事实发生在舞会上」为真，也就是要对两个集合取交——我们得到了所有「在舞会上，某人亲吻了 Bob」的集合。这就是 VP 的真值集合。

在逻辑学和语言学中，我们把需要研究（其意义）的语言称为对象语言(object language)，用于描述（其意义）的语言称为元语言(meta language)。比如在上面的描述中，对象语言是英语，而元语言是汉语。读者可以发现上文的书写非常复杂难懂。这是因为我们用了一门自然语言（汉语）做元语言，而自然语言天然地有歧义性，想把事情说清楚就须得费一番功夫。

大家不喜欢费工夫，于是就希望能用一种明确的语言来做元语言。什么样的语言是明确的呢？大家自然就想到了数学的语言，逻辑的语言。比如我们可以用集合论的语言改写上面的说明。记 $T(\text{X})$ 为以 X 为根的句法树对应的真值集合，则上面的推导过程可以简单的写成：

• $T(\text{V}) = \{(u, v, w) \mid u\text{ kissed } v \text{ at } w\}$
• $T(\text{V'}) = \{(u, v, w) \mid (u, v, w) \in T(\text{V}) \land v = \text{Bob} \}$
• $T(\text{VP}) = \{(u, v, w) \mid (u, v, w) \in T(\text{V'}) \land w = \text{dance party} \}$
• $T(\text{TP}) = \{(u, v, w) \mid (u, v, w) \in T(\text{VP}) \land u = \text{Alice} \}$

观察这个过程，我们首先考虑句法树底部的一个较小范畴（它有着最大的真值集合）。随后再根据其他句法范畴的真值集合，逐层确定元组的每个参数，似乎是用一些 Filter(过滤器) 不断地筛去一些不合法的元素，生成 Filter 的过程又需要近乎 Currying(柯里化) 的参数捕捉——也就是说组合语义计算天然地是函数式的。

恐怕这也就是语言学家们喜欢使用 $\lambda$-演算(lambda calculus) 作为元语言的原因了。下面我们对上述例子给出 $\lambda$-演算形式的表述（想必熟悉函数式编程的读者一定能读懂下面的简单情形，我们将在下一节中介绍更多细节）。

• 在 V 处的真值计算可以用 $\lambda$表达式 $\lambda v.\lambda w.\lambda u. \text{kiss}(u, v, w)$ 表示

• 上溯一级到 V’ 处时则将 NP apply 到表达式上，得到

  $\begin{aligned} & \lambda v.\lambda w.\lambda u. \text{Kiss}(u, v, w) (\text{Bob}) \\ =& \lambda w.\lambda u. \text{Kiss}(u, \text{Bob}, w) \end{aligned}$

• 再上溯一级到 VP 处，类似地 apply 得

  $\begin{aligned} & \lambda w.\lambda u. \text{Kiss}(u, \text{Bob}, w)(\text{dance party}) \\ =& \lambda u. \text{Kiss}(u, \text{Bob}, \text{dance party}) \end{aligned}$

• 继续向上即有

  $\begin{aligned} & \lambda u. \text{Kiss}(u, \text{Bob}, \text{dance party})(\text{Alice}) \\ =& \text{Kiss}(\text{Alice}, \text{Bob}, \text{dance party}) \end{aligned}$

最终句子的真值即逻辑谓词(predicate) $\text{Kiss}(u, v, w)$ 的真值，其真值集合就和上文论述的一样。由于这个例句相当简单，我们没有涉及较复杂的情况。在下一节介绍完 lambda calculus 相关的内容后，我们再看相关的例子。

话说回来，各位汉语读者发现逻辑的「谓词」和语言的「谓语」都是同一个 Predicate 时，是否有种灵光一现的感觉呢？

Lambda Calculus

上节说到，一些语言学家认为语义是可以通过计算(Computation) 得到的。$\lambda$-calculus 就是一种试图描述何为「计算」的一种形式系统，其本质是一种纯粹的形式语言(Formal Language)。

形式语言首先是一种完全结构化（也称语法化）的语言，语言中的每个成分都可以给出结构化的表示。比如在上一节中的 Alice kissed Bob at the dance party 一句，在我们的句法规则体系下就是完全结构化的——它句法树上的每个子结构都是合理的语言片段（kissed bob, at the party, kissed bob at the party）。

一种形式语言学的信仰认为，在人类语言中应当只有有限的一些合法结构。而无论多么复杂的长难句，也只是通过有限结构的无限嵌套、堆叠产生的。比如对于一个英语短语：

an intelligent, attractive and meritorious girl

在我们的句法体系下，可以给出这样的句法树：

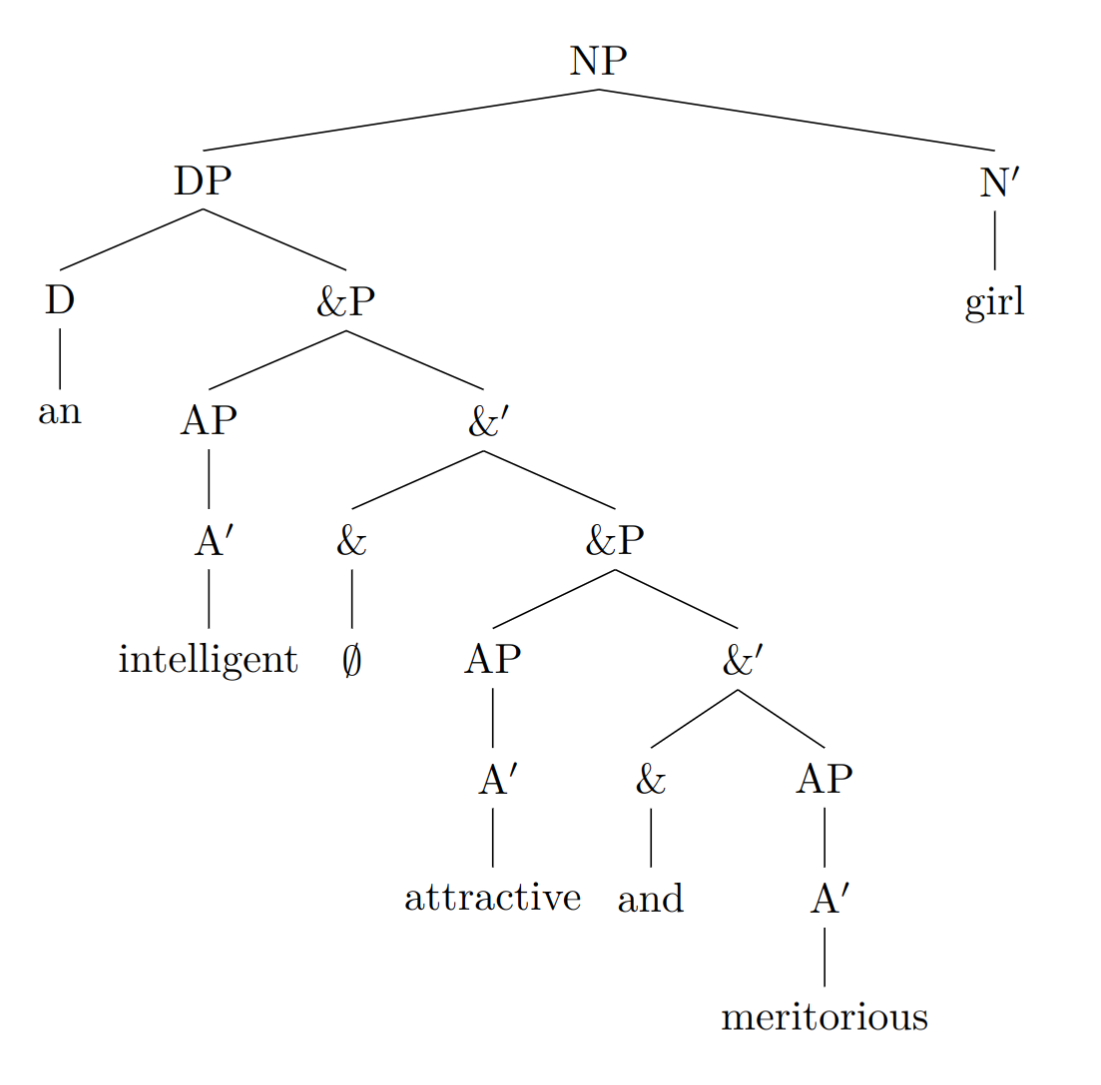
这里 AP 为表示形容性短语的句法结构，&P 是用于表示并列的句法结构（该结构在学界尚有争议，不过我们暂且接受这一用法）。可以想象的是，如果我们想要给 girl 冠以更多的形容词或形容结构，也只需在这个句法树上嵌套、堆叠更多相似的 $\text{\&P} \to \text{AP \&'}$，并适当地修改 AP 的内容就可以了。既然这样，那么赞美女孩子这样一个顶尖困难的工作就变得结构化了，显得直观而容易。

当然，在自然语言中存在很多难以结构化考虑的句子，关于合法结构有限性、最简性的信仰仍然需要大量的实例与理论修正。为了证明他们的信仰，形式学派的语言学家还需要付出许多的努力。而反观逻辑与计算的世界，许多人工制造语言则生来即有纯粹的、结构化的性质——比如我们即将介绍的 $\lambda$-calculus，以及下面几节会介绍的一阶逻辑语言、程序设计语言等。这也就是所谓的形式语言。

---

具体到 $\lambda$-calculus，如果我们用 $E$ 表示所有可能的 $\lambda$-calculus 语言中的句子(即 $\lambda$-expression)，那么 $E$ 只可能由四个简单的语法范畴构成。这里我们给出 $E$ 的产生式如下：

$\begin{aligned} \text{(Identifier)} \qquad E &\to \mathbf{id}\\ \text{(Grouping)} \qquad E &\to (E) \\ \text{(Abstraction)} \qquad E &\to \lambda~\mathbf{id}.E \\ \text{(Application)} \qquad E &\to E ~ E \end{aligned}$

这里每一行的产生式规则的含义是，任何时候箭头左侧的 $E$ 都可以转写成右侧的形式并做进一步转写。最左侧的文字是产生式的名称。这里 $\mathbf{id}$ 一般是 $x, y, z$ 等小写字母。我们会在第四章里介绍更多关于产生式的内容。为了给读者留下一个直观的印象，这里我们举出一个例子

$\lambda x.\lambda y.((\lambda z.y~z)~x)$

我们可以按使用产生式进行转写的顺序画出这棵表达式对应的语法树：

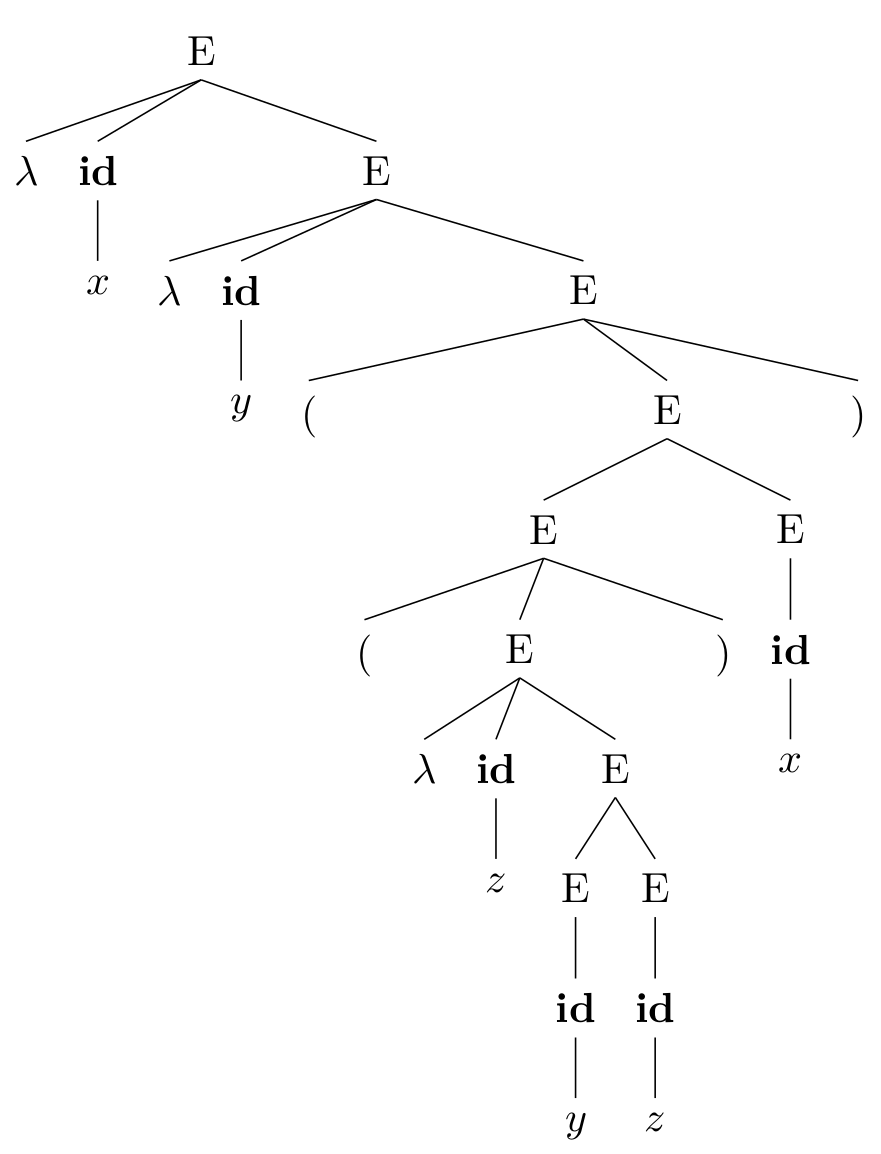
接下来我们先在直觉上理解一下几个语法结构。

Grouping 只用于指示运算优先级，这里不展开讨论。

Identifier 可以简单而深刻地理解为「名字」。在上一节中的 Alice kissed Bob at the dance party 一句里，Alice 和 Bob 就是两个抽象的名字。你可以用这两个名字代表世界上任意什么人，然后代入这个句子检查其真值。在句子里我们用了 Alice kissed Bob 而不是 Alice kissed Alice，也仅仅是在表示：亲吻的施事与受事未必同一个人而已。

Abstraction 与 Application 两部分，又实际上构成了我们熟悉的函数。比如在初等数学的语言中，

$f(x) = x + 1$

表达了一个名字为 $f$ 的函数，该函数可以接受一个参数 $x$，且计算得到 $x + 1$ 作为函数值。这件事就叫 Abstraction，它把一个计算过程抽象为了一个函数。

比如我们还可以写

$f(2) = 2 + 1 = 3$

这就是把 $2$ 代入到名字为 $f$ 的函数中，这个过程就叫做 Application。

我们可以等价地用 $\lambda$-calculus 写出同样的 Application 过程：

$\begin{aligned} (\lambda x. x + 1) (2) = 2 + 1 = 3 \end{aligned}$

注意到 $\lambda$-calculus 里，所有函数都是匿名的。也就是说这里 $\lambda x. x + 1$ 也就是上面名字为 $f$ 的函数。（虽然我们的语法中没有引入自然数和加号，但之后我们会展示这是不必要的，存在等价的替代写法）

形式上来说，$(\lambda x. E_1) ~ E_2$ 这样的 Application 的过程，就是在没有名字冲突的情况下，把 $E_1$ 中出现的所有 $x$ 使用 $E_2$ 替换(substitution)，记作 $E_1[E_2/x]$。

当然，既然我们正要定义一种形式语言，也就需要精确地、形式地定义替换等过程。结构归纳就可以帮助我们完成这种定义。结构归纳法是一般化的数学归纳法。我们知道，数学归纳法之所以能应用在自然数上，就是因为自然数的结构中容纳了一个良序。我们又可以想到：自然数其实就是具有前后关系的单向链表。而既然这样的结构里存在良序，其他的结构里也自然可以存在良序，进而可以在其他的结构里应用归纳法。比如在一个递归定义的树形结构里，比如在 $\lambda$-calculus 的结构里。接下来看一个例子：

首先引入符号 $\equiv$ 表示两个表达式逐字符一致。记号 $E\{y / x\}$ 表示变量重命名(renaming)，即把 $E$ 中的所有变量 $x$ 的名字改为 $y$ 得到的字符串。那么有

$E\{y / x\} = \begin{cases} y & E \equiv x \\ z & (E \equiv z) \land (x \not\equiv z) \\ (E'\{y / x\}) & E \equiv (E') \\ \lambda y. E'\{y / x\} & E \equiv \lambda x.E' \\ \lambda z. E'\{y / x\} & (E \equiv \lambda z.E') \land (x \not\equiv z) \\ E_1\{y / x\} ~ E_2\{y / x\} & E \equiv E_1~E_2 \end{cases}$

这里 $\land$ 表示逻辑与，$a \not\equiv b$ 是「表达式 $a \equiv b$ 为假」的简略写法。可以发现我们通过由上到下讨论了 $E$ 分别为 Identifier, Grouping, Abstraction, Application 的四种不同情况，覆盖了 $E$ 的所有结构，并对于每种结构给出了不同的处理方式。从而，我们通过递归地对一个 $\lambda$ 表达式的子树进行修改的方式，完成了整个语法树的修改。

这里给出一个简单的重命名例子。考虑求 $(\lambda x.x~ z)\{y/ x\}$ 时，结构树则如下图所示：

结构归纳还可以用于递归地定义与结构相关的函数。比如，我们考虑用 $FV(E)$ 表示表达式 $E$ 中所有自由变量的集合，那么可以有定义

$FV(E) = \begin{cases} \{x\} & E \equiv x \\ FV(E') & E \equiv (E') \\ FV(E') \setminus \{x\} & E \equiv \lambda x.E' \\ FV(E_1) \cup FV(E_2) & E \equiv E_1~E_2 \end{cases}$

这里 $\setminus$ 是求差集，$\cup$ 是求并集。所谓的自由变量也就是在表达式中出现，但是又没有被外层的 Abstraction 领属的一些变量。这里同样给出一个例子，考虑求 $FV(\lambda x.x~ z)$，我们有这样的语法树，树上节点标记了子树中 $FV$ 集合的求解结果。

有了上面两个定义之后，我们终于可以考虑着手定义 Application 过程中的替换了。对于替换过程 $E_1[E_2/ x]$，我们讨论 $E_1$ 的形式：

$E_1[E_2/ x] = \begin{cases} E_2 & E_1 \equiv x \\ y & E_1 \equiv y \land y \not\equiv x \\ (E_3[E_2 / x]) & E_1 \equiv (E_3) \\ \lambda x.E_3 & E_1 \equiv \lambda x.E_3 \\ \lambda y.(E_3[E_2/x]) & (E_1 \equiv \lambda x.E_3) \land (y \not\equiv x) \land (y \not\in FV(E_3)) \\ \lambda z. (E_3 \{z / y\}[E_2/x]) & (E_1 \equiv \lambda x.E_3) \land (y \not\equiv x) \land (y \in FV(E_3)) \land (z \equiv \texttt{freshID}()) \\ (E_3[E_2/x])(E_4[E_2/x]) & E_1 \equiv E_3~E_4 \end{cases}$

这里函数 $\texttt{freshID}$ 会返回一个在表达式中从未出现过的 Identifier。注意到 Abstraction 替换的定义需要额外的技巧以考虑领属关系导致的作用域变化，或换言之，我们需要特别考虑子树内外的 $x$ 在不同语境中所指变量不同的情形。这里我们姑且举出一个替换的例子：

$\begin{aligned} & (\lambda x. y~x)[(\lambda z. x~ z) / y] \\ \equiv & \lambda x. ((y~x) [(\lambda z. x~ z) / y]) \\ \equiv & \lambda x. (y[(\lambda z. x~ z) / y] ~ x[(\lambda z. x~ z) / y]) \\ \equiv & \lambda x. ((\lambda z. x ~ z) ~x) \end{aligned}$

---

在形式化定义了替换之后，我们又可以进一步给出 $\beta$-reduction 的定义。

这种 reduction 即把一个 $\lambda$-表达式通过“代入函数参数”的方法，在形式上变换为另外一个不含“函数”的结果形式。我们知道，在初等数学的函数里，代入参数的过程也就是计算函数值的过程。$\beta$-reduction 其实也就定义了 $\lambda$-表达式的计算过程。

所谓计算，也可以认为是花费代价将事物变得更本质的过程。比如通过将 $x=1$ 代入 $x+1$ 得到 $2$ 这样的计算过程中：首先我们有一个内涵相当大的表达式 $x+1$（可能是任意一个数），通过计算之后则得到了内涵最小的、一个单独的数字 2。背景为信息论或物理学的一些学者认为，计算就是花费一番功夫，将表达式所能表达的信息（内涵）变小的过程——也就是消耗能量使熵减少的过程。甚至有基于麦克斯韦妖假想，推导出计算 1 bit 信息所需最小能量的工作（也就是 Landauer's principle）——这也暗合 reduction 一词的自然语言语义。

抛开这些玄之又玄的内容不谈，总之 $\beta$-reduction 可以视为在一些方面对 $\lambda$-表达式的简化（尽管最后的形式可能变得更长）。接下来我们给出它的形式化定义。

我们用符号 $E_1 \to E_2$ 表示表达式 $E_1$ 经过一步 $\beta$-reduction 后得到的可能结果为 $E_2$。其中每一步 reduction 都可以应用下面的任意一条规则：

$\begin{aligned} (\text{cong}_1) \qquad & \dfrac{M \to M'}{M ~ N \to M' ~ N} \\[8pt] (\text{cong}_2) \qquad & \dfrac{N \to N'}{M ~ N \to M ~ N'} \\[8pt] (\beta) \qquad & \dfrac{\phantom{M}}{(\lambda x. M)~N \to M[N/x]} \\[8pt] (\xi) \qquad & \dfrac{M \to M'}{\lambda x . M \to \lambda x. M'} \end{aligned}$

左侧括号是规则的名称，右侧由一条长横线组织的式子就是规则的内容。在横线上方的式子是应用该规则的前提，空的横线则表示该规则可以在任何情况应用。

我们举出一个例子：

$\begin{aligned} & (\lambda f. \lambda x . f ~ x)~(\lambda y. y ~ y) \\ \to & \lambda x . (\lambda y. y ~ y) ~ x & \text{by rule } \beta \phantom{\xi} \\ \to & \lambda x . x ~ x & \text{by rule } \xi \phantom{\beta} \end{aligned}$

考虑不停地使用规则，直到没有规则可用后，我们就可能得到一个「结果」。这个结果被称作 Normal Form，它不含有 $\beta$-redex，也就是形如 $(\lambda x. M)~N$ 的子结构。也就是说在 Normal Form 中，所有可以代入的参数已经完全被代入了。

刚刚说到 $\beta$-reduction 的每一步推导都可以使用上面的任意一个规则。一个重要的结论是：无论以何种顺序使用规则直到无规则可用，所得的 Normal From（假如能得到一个的话）总是相同。这一性质就称作 Confluence(合流性)。它有一个更吓人的名字叫做 Church-Rosser Property。

比如考虑式 $(\lambda f. \lambda x. f (f ~ x))~(\lambda y. y + 1)~ 2$，我们可以有两种不同的 reduction 方式：

$\begin{aligned} & (\lambda f. \lambda x. f (f ~ x))~(\lambda y. y + 1)~ 2 \\ \to & \lambda x. (\lambda y. y + 1) ((\lambda y. y + 1) ~ x) ~ 2 \\ \to & \lambda x. (\lambda y. y + 1) (x + 1) ~ 2 \\ \to & (\lambda x. x + 1 + 1) ~ 2 \\ \to & 2 + 1 + 1 \end{aligned}$

$\begin{aligned} & (\lambda f. \lambda x. f (f ~ x))~(\lambda y. y + 1)~ 2 \\ \to & \lambda x. (\lambda y. y + 1) ((\lambda y. y + 1) ~ x) ~ 2 \\ \to & \lambda x. (\lambda y. y + 1) (x + 1) ~ 2 \\ \to & \lambda x. (\lambda y. y + 1) (2 + 1)\\ \to & 2 + 1 + 1 \end{aligned}$

这在初等数学中几乎是直觉。不过我们既然在讨论一切计算的基础，讨论纯形式的话题，这一性质当然就具有相当的重要性。这一证明实在超出了这篇文章的内容，感兴趣的读者可以按关键词查阅相关资料。

刚刚我们反复强调「如果能得到一个结果」则是因为对于一些特别的式子，按某个特定顺序应用规则的话，reduction 永远不会终止。比如对于式子 $(\lambda u. \lambda v. v) ((\lambda x. x~ x)(\lambda x. x~ x))$，假如我们直接在最外层应用 $\beta$ 规则，就直接得到了结果 $\lambda v. v$；而如果不停地使用 $\text{cong}_2$，则会永远卡死在这个形式上。

所以尽管我们有 confluence 这样强的性质，由于特定式子的上述特定性质，在实际应用中往往会规定一个使用规则的顺序。一般有两种：

• Normal Order，总是在表达式的最左侧、$\lambda$ 函数嵌套的最外层使用 $\beta$ 规则。
• Applicative Order，总是在表达式的最左侧、$\lambda$ 函数嵌套的最里层使用 $\beta$ 规则。

在生产环境的程序设计语言里，这两种顺序就分别形成了使用 Normal Order 的 call-by-name 风格语言（如 ALGOL 60）；以及使用 Applicative Order 的 call-by-value 语言（如 C, Java 等）；当然也存在不严格地按某一种顺序的折中方案，call-by-need 语言（如 Haskell, R 等）。

---

终于说到一点应用部分了。$\lambda$-calculus 看起来如此地简单，我们却说它能描述何为「计算」，这似乎是很不寻常的一件事情——的确如此，这件事也就是大名鼎鼎的邱奇-图灵论题(Church-Turing Thesis)。

该论题揭示了两件事情：

• $\lambda$-演算(Lambda Calculus)，图灵机(Turing machine)，一般递归函数(General Recursive Function) 在表达能力上是等价的。
  这三项工作都在 1936 发表，分别是由 Church；Turing；Gödel，Herbrand，Kleene 完成。这是五个非同小可的人物——在今天的数理逻辑、计算机、自动机理论学界，每个人的名字都各自对应一个重要的奖项。其中图灵奖和哥德尔奖分别是计算机科学和理论计算机科学界的最高奖。
• 任何可计算过程，都可以用上面的任意一个模型表达。

本文不打算深入探讨关于可计算性理论的相关问题（以后可能会有一篇专门的文章），这里我们给出两个简单而深刻的例子以展现 $\lambda$-calculus 强大的表达能力。

Case 01

我们先看一个用 $\lambda$-calculus 表达自然数运算的例子（这种构造也被称作 Church Numeral）。

我们定义：

$\begin{aligned} \bar{0} &= \lambda f. \lambda x. x \\ \bar{1} &= \lambda f. \lambda x. f ~ x \\ \bar{2} &= \lambda f. \lambda x. f ~ f ~ x \\ &\vdots \end{aligned}$

即 $f$ 被应用到 $x$ 上的次数代表了自然数的数值。下面给出自然数的常见运算对应的表达式（这里 $\text{ADD, MUL, POW}$ 是为了简化论述，给匿名的表达式人为赋予的名字）：

• 加法 $\text{ADD} \equiv \lambda n. \lambda m. \lambda f. \lambda x. n~f~(m~f~x)$，即在 $x$ 上首先应用 $m$ 次 $f$，再应用 $n$ 次 $f$。比如

  $\begin{aligned} \text{ADD 2 3} & \equiv (\lambda n. \lambda m. \lambda f. \lambda x. n~f~(m~f~x))~ (\lambda f. \lambda x. f ~ f ~ x)~ (\lambda f. \lambda x. f ~ f ~ f ~ x) \\ & \to (\lambda m. \lambda f. \lambda x. (\lambda f. \lambda x. f ~ f ~ x)~f~(m~f~x))~ (\lambda f. \lambda x. f ~ f ~ f ~ x) \\ & \to (\lambda m. \lambda f. \lambda x. (\lambda x. f ~ f ~ x) ~(m~f~x))~ (\lambda f. \lambda x. f ~ f ~ f ~ x) \\ & \to (\lambda m. \lambda f. \lambda x. f ~ f ~ (m~f~x)) ~ (\lambda f. \lambda x. f ~ f ~ f ~ x) \\ & \to \lambda f. \lambda x. f ~ f ~ ((\lambda f. \lambda x. f ~ f ~ f ~ x)~f~x)) \\ & \to \lambda f. \lambda x. f ~ f ~ f ~ f ~ f ~ x \equiv \text{5} \\ \end{aligned}$

• 乘法 $\text{MUL} \equiv \lambda n. \lambda m. \lambda f. n ~(m ~ f)$，即使用 $f$ 在 $x$ 上已应用 $m$ 次的表达式作为 $n$ 的参数传入，从而重复这个式子 $n$ 次，也就得到了 $n \times m$ 的结果。比如

  $\begin{aligned} \text{MUL 2 3} & \equiv (\lambda n. \lambda m. \lambda f. n ~(m ~ f)) ~ (\lambda f. \lambda x. f ~ f ~ x)~ (\lambda f. \lambda x. f ~ f ~ f ~ x) \\ & \to (\lambda m. \lambda f. (\lambda f. \lambda x. f ~ f ~ x) ~(m ~ f)) ~ (\lambda f. \lambda x. f ~ f ~ f ~ x) \\ & \to (\lambda m. \lambda f. (\lambda x. (m ~ f) ~ (m ~ f) ~ x)) ~ (\lambda f. \lambda x. f ~ f ~ f ~ x) \\ & \to \lambda f. \lambda x. ((\lambda f. \lambda x. f ~ f ~ f ~ x) ~ f) ~ ((\lambda f. \lambda x. f ~ f ~ f ~ x) ~ f) ~ x \\ & \to \lambda f. \lambda x. (\lambda x. f ~ f ~ f ~ x) ~ (\lambda x. f ~ f ~ f ~ x) ~ x \\ & \to \lambda f. \lambda x. f ~ f ~ f ~ f ~ f ~ f ~ x \equiv \text{6} \\ \end{aligned}$

• 乘方(POW) $\lambda n. \lambda m. n ~ m$，与乘法的想法类似，返回 $m^n$ 的结果，例子姑且略去。

Case 02

我们再看一个布尔代数的例子。布尔代数就是通过与或非等逻辑运算，计算复杂逻辑命题真值的一种代数系统。

我们定义

• $\text{T} \equiv \lambda x. \lambda y. x$ 表达「真」的含义。
• $\text{F} \equiv \lambda x. \lambda y. y$ 表达 「假」的含义。

那么 $\lambda a. \lambda b. a~b~F$ 就表达了「与」的意义，我们给这个表达式以名字 $\text{AND}$，可以验证如下：

$\begin{aligned} \text{AND T T} & \equiv (\lambda a. \lambda b. a~b~(\lambda x. \lambda y. y)) ~ (\lambda x. \lambda y. x) ~ (\lambda x. \lambda y. x) \\ & \to (\lambda b. (\lambda x. \lambda y. x)~b~(\lambda x. \lambda y. y)) (\lambda x. \lambda y. x) \\ & \to (\lambda x. \lambda y. x)~(\lambda x. \lambda y. x)~(\lambda x. \lambda y. y) \\ & \to (\lambda y. (\lambda x. \lambda y. x))~(\lambda x. \lambda y. y) \\ & \to (\lambda x. \lambda y. x) \equiv \text{T} \end{aligned}$

$\begin{aligned} \text{AND T F} & \equiv (\lambda a. \lambda b. a~b~(\lambda x. \lambda y. y)) ~ (\lambda x. \lambda y. x) ~ (\lambda x. \lambda y. y) \\ & \to (\lambda b. (\lambda x. \lambda y. x)~b~(\lambda x. \lambda y. y)) (\lambda x. \lambda y. y) \\ & \to (\lambda x. \lambda y. x)~(\lambda x. \lambda y. y)~(\lambda x. \lambda y. y) \\ & \to (\lambda y. (\lambda x. \lambda y. y))~(\lambda x. \lambda y. y) \\ & \to (\lambda x. \lambda y. y) \equiv \text{F} \end{aligned}$

我们略去式子 $\text{AND F T}$ 与 $\text{AND F F}$ 的 reduction 过程，读者可以试着自己推导一下，得到的结果当然是正确的。通过类似的方式，我们可以定义「或」运算为 $\lambda x. \lambda y. (x ~ \text{T} ~ (y ~ \text{T F}))$，「非」运算为 $\lambda b. (b ~\text{F T})$ 等等各类逻辑运算，完整地表达布尔代数。

上面的构造看起来有些不可思议。我们姑且给出一个解释吧：T F 的构造或许暗合于最古老的哲学：

To say of what is that it is not, or of what is not that it is, is false, while to say of what is that it is, and of what is not that it is not, is true.

(Aristotle, Metaphysics 1011b25)

这句话并没有太好的中文译法，而想必绝大多数读者都读不了希腊文字，因此折中地给出一个英语版本。

Mathematical Logic

在开始本节具体介绍之前，我们先从历史说起。上一节中，我们给出了 $\lambda$-calculus 的形式化描述，用机械的、有限的、符号层面的规则阐释了「意义」，真正严谨地定义了一种语言。像是“形式化”、“意义”、“真正严谨”这样的字眼，经历几千年的风云变幻，我们今天听来仍然有些目眩神迷、情迷意乱。

在古代希腊，逻各斯(λόγος) 的意义首先是话语，之后才是我们熟知的理性、推理、原理。这个能指的双关非常深刻：可以说，人类理性要想真正证明自己的伟大，首先应该战胜的就是语言的不确定性。

人们一般说人文学科是不严格的。这是因为面对同一文本，我们总可以从不同的角度进行阐释，从而得到不同的含义。同时，这些阐释本身也可以由他人再另作阐释。而在阐释的链条中，文本的意义就上下飘忽，不能严格地确定。但我们自然可以转念一想，这样由语言阐释造成的误解链条，完全可能在任何一门学科中存在——比如追求严格性、客观性、真理性，被视为人类理性精华的数学。

因此摆在我们面前的首要问题，就是如何将语言、特别是数学的语言严格化。

在古希腊，亚里士多德的严格三段论成为基本的推理方法。而欧几里得使用这样的演绎方法，从五条事实出发为我们展示了一个几乎完备的几何世界。这被称作公理化方法，是形式化方法的一种，我们相信这样的方法是相对严格的。当然，欧几里得的几何公理系统并没有完全严格化，我们之后会讨论这个问题。

更之后的进展在十七世纪，笛卡尔提出了「普遍数学」的设想：认为可能存在这样一个系统，由有限的公理可以演绎出不止于几何、所有数学知识、以致于全部的人类知识。另一个表述则被浪漫地称作「莱布尼兹之梦」，少年时代的莱布尼兹畅想：可能存在这样一张字母表，我们可以从中发展出一种语言（符号系统），接着仅凭符号演算，就能判定该语言中的哪些句子为真。

到十九世纪，皮亚诺给出了算术系统的公理化描述。紧接着弗雷格给出了一个公理化的逻辑系统，并用该系统导出了皮亚诺算术。这项工作非常重要，可以视为现代数理逻辑的开端。同时，这直接影响了罗素的《数学原理》与维特根斯坦的《逻辑哲学论》——此后就有了分析哲学。

最终到了二十世纪，在 1920 年，我们迎来了轰轰烈烈的希尔伯特计划。其目标是为所有的数学提供一个形式化的、一致的、完备的符号系统，成为所有数学工作的基础。

在本节中，我们从弗雷格的工作出发，介绍一阶谓词逻辑语言并试图描述皮亚诺算术。接着我们会介绍 Gentzen 的自然推理系统，用纯语法的方法作一阶谓词逻辑的推理。稍后我们会讨论该系统的一些重要性质。最后我们简单介绍哥德尔不完备性定理，该定理最终宣告了希尔伯特计划的破产。

正如宋方敏老师所说，在上面这样的历程里，「数理逻辑见证了人类的伟大与无助」。

---

一阶谓词逻辑语言，实际上就是通过一些纯形式的方式来定义逻辑。

很自然地，我们会格外关注这些符号的定义：

• 逻辑连接词 $\land~\lor~\neg~\to$，即与、或、非、蕴含
• 逻辑量词 $\forall~\exists$，即全称、存在

除了这几个关键的符号，我们自然也需要一些其他的东西才能写出合法的命题。这又包括

• 变元集 $V$，可以视作所有合法变量 Identifier 的集合。包含可数无穷个元素 $x_0, x_1, \dots, x_n, \dots$
• 常元集 $\mathscr{L}_c$，所有常量 Identifier 的集合，包含可数个元素。
• 函数集 $\mathscr{L}_f$，可数个函数符号 $f_0, f_1, \dots$ 的集合。正整数 $\mu(f_i)$ 表示函数 $f_i$ 的元数。
• 谓词集 $\mathscr{L}_P$，可数个谓词符号 $P_0, P_1, \dots$ 的集合。正整数 $\mu(P_i)$ 表示函数 $P_i$ 的元数。
• 等词 $\equiv$，一个特殊的二元谓词，表示逐字符的一致。
• 辅助符 $(~)~.~,$

这里常元集、函数集、谓词集的并记作 $\mathscr{L}$，也即非逻辑符集合。

做好了这些定义的准备工作，我们就可以给出一阶谓词逻辑语言的形式语法了：

$\begin{aligned} T &\to v & v \in V \\ T &\to c & c \in \mathscr{L}_c \\ T &\to f(T_1, T_2, \dots, T_{\mu(f)}) & f \in \mathscr{L}_f \\ F &\to P(T_1, T_2, \dots, T_{\mu(P)}) & P \in \mathscr{L}_P \cup \{\equiv\} \\ F &\to (\neg F) \\ F &\to (F * F) & * \in \{\land, \lor, \to\} \\ F &\to Q v.F & Q \in \{\forall, \exists\}, v \in V \\ \end{aligned}$

这里 $T$ 是项(Term) 的缩写，$F$ 是公式(Formula) 的缩写。接下来我们看一个具体的例子。

通过定制 $\mathscr{L}$ 可以定义不同的语言。比如我们可能想要定义初等算数语言 $\mathscr{A}$，则需要有

• $\mathscr{A}_c = \{0\}$，含有一个表示最小的自然数记号；
• $\mathscr{A}_f = \{S, +, \cdot\}$，三者分别为求后继的一元函数、求和的二元函数、求积的二元函数；
• $\mathscr{A}_P = \{<\}$，含有一个指示小于关系的二元谓词。

而初等算数语言的一个公式可以是：

$\forall x.(x < S(x) \land \exists y. <(x,y))$

对应的句法树如下

非形式地说，这个公式含义是：对于任意的 $x$ 都有以下两件事同时成立：$x$ 小于它的后继，并且存在 $y$ 使得 $x$ 小于 $y$。我们有多种途径去形式化这样的含义。本章接下来我们将采用英语和集合的运算符号作为元语言，简单介绍两种形式化的方式。

---

语义可满足

第一种，也是比较直观的一种方式是引入该语言所实际描述的结构和模型。先看定义：

结构(Structure)

对于一个语言 $\mathscr{L}$，它的一个结构 $\mathbb{M}$ 是一个二元组 $(M, I)$ 满足

• $M$ 被称作论域(domain)，是一个非空集合。语言中涉及的变元、常元最终都会落实到 $M$ 中的一个特定元素。

• $I$ 是一个定义域为 $\mathscr{L}$ 的映射。它实际上起到了将常元集、函数集、谓词集从整个定义域中分离开的作用。为达到这样的效果，它需要满足四个性质：

  • For all $c \in \mathscr{L}_c$, there is $I(c) \in M$

    即对于给定的常元符 $c$，$I$ 可以将它映射到 $M$ 中的一个具体元素。

  • For all $f \in \mathscr{L}_f$ with $\mu(f) > 0$, there is $I(f): M^{\mu(f)} \to M$

    即对于给定的函数符 $f$，$I(f)$ 又是一个映射，可以将给定的 $\mu(f)$ 个参数组成的有序对映射到 $M$ 中的一个具体元素。

  • For all $P \in \mathscr{L}_P$ with $\mu(P)=0$, there is $I(P) \in \mathbf{B}$

    这里 $\mathbf{B} = \{\texttt{true}, \texttt{false}\}$ 是真假值的集合。即对于零元谓词 $P$，$I$ 直接将它映射到一个真假值。

  • For all $P \in \mathscr{L}_P$ with $\mu(P)>0$, there is $I(P) \subseteq M^{\mu(P)}$

    即对于一个多元谓词 $P$，$I$ 会将它映射到一个 $\mu(P)$ 元的集合，该集合就是谓词的真值集合。换言之，所有在该集合中的有序对会使谓词求得真值；而不在该集合中的有序对会使谓词求得假值。

    注意这和第一章中自然语言谓语的真值集合概念一致。

模型(Model)

模型 $\mathcal{M}$ 是一个二元组 $(\mathbb{M}, \sigma)$，这里 $\mathbb{M}$ 是一个结构，而 $\sigma$ 是该结构上的一个赋值。所谓赋值就是给变元集中的每个变元制定一个论域 $M$ 中的元素作为对应，也即是说它是一个类型为 $\sigma: V \to M$ 的映射。

在一个给定的模型下，我们就可以通过将项解释到论域中的元素，再将公式中的结构解释到具体的真假值的方式，在该模型下确认公式的真假。下面就给出这一过程的形式化：

• 项的解释

  $T_{\mathbb{M}[\sigma]} = \begin{cases} \sigma(x) & T \equiv x \\ I(c) & T \equiv c \\ I(f)({T_1}_{\mathbb{M}[\sigma]}, \dots {T_{\mu(f)}}_{\mathbb{M}[\sigma]}) & T \equiv f(T_1, \dots, T_{\mu(m)}) \end{cases}$

• 公式的解释

  首先引入记号

  $\sigma[x:=e](v) = \begin{cases} \sigma(v) & v \not= x \\ e & v = x \end{cases}$

  用于表示修改给定的赋值 $\sigma$ 的一个映射对得到的新赋值。利用该符号，我们可以定义公式的解释如下：

  $\begin{aligned} {P(T_1, \dots, T_{\mu(P)})}_{\mathbb{M}[\sigma]} &= \begin{cases} \texttt{true} & \left( {T_1}_{\mathbb{M}[\sigma]}, \dots, {T_{\mu(P)}}_{\mathbb{M}[\sigma]} \right) \in I(P) \\ \texttt{false} & \text{otherwise} \end{cases} \\ (\neg F)_{\mathbb{M}[\sigma]} &= \begin{cases} \texttt{true} & F_{\mathbb{M}[\sigma]} = \texttt{false} \\ \texttt{false} & \text{otherwise} \end{cases} \\ (F_1 \to F_2)_{\mathbb{M}[\sigma]} &= \begin{cases} \texttt{true} & \text{(${F_1}_{\mathbb{M}[\sigma]} = \texttt{true}$ and ${F_2}_{\mathbb{M}[\sigma]} = \texttt{true}$) or ${F_1}_{\mathbb{M}[\sigma]} = \texttt{false}$} \\ \texttt{false} & \text{otherwise} \end{cases} \\ \vdots \quad &\phantom{=} \qquad \vdots \\ (\forall x.F)_{\mathbb{M}[\sigma]} &= \begin{cases} \texttt{true} & \text{For all $e \in M$, there is $(F_{\mathbb{M}[\sigma[x:=e]]} = \texttt{true})$} \\ \texttt{false} & \text{Some $e \in M$ would make $(F_{\mathbb{M}[\sigma[x:=e]]} = \texttt{false})$} \end{cases} \\ (\exists x.F)_{\mathbb{M}[\sigma]} &= \begin{cases} \texttt{true} & \text{Some $e \in M$ would make $(F_{\mathbb{M}[\sigma[x:=e]]} = \texttt{true})$ } \\ \texttt{false} & \text{For all $e \in M$, there is $(F_{\mathbb{M}[\sigma[x:=e]]} = \texttt{false})$ } \end{cases} \end{aligned}$

  这里省略了一些可以类推出的简单情形。

至此，我们完成了「解释」的定义，也由此得到了一个可以判断公式真假的工具。不过想要对公式进行语义证明，我们还需要引入一些辅助记号。

• $\mathbb{M} \models_\sigma F$ means $F_{\mathbb{M}[\sigma]} = \texttt{true}$
• $\mathbb{M} \models F$ means for all $\sigma$ on $\mathbb{M}$, there is $\mathbb{M} \models_\sigma F$
• $\models F$: means for all model $(\mathbb{M}, \sigma)$, there is $\mathbb{M} \models_\sigma F$

这里符号 $\models$ 可以视作在「语义上能导出」的含义，或者可以用术语称可满足(satisfiable)。最后一个记号也可读作 $F$ 永真(valid)。

我们看两个用上面这样的形式方法进行证明的例子：

Case 01

证明下面的式子是永真的：如果「并非对于所有 $x$ 都有 $F$ 成立」，那么「存在 $x$ 使得 $F$ 不成立」。

$\begin{aligned} & \models \neg(\forall x. F) \to \exists x. (\neg F) \\ \iff & \text{For all $(\mathbb{M}, \sigma)$},~ \mathbb{M} \models_{\sigma} \neg(\forall x. F) \to \exists x. (\neg F) \\ \iff & \text{For all $(\mathbb{M}, \sigma)$},~ \left(\neg(\forall x. F) \to \exists x. (\neg F)\right)_{\mathbb{M}[\sigma]} = \texttt{true} \\ \iff & \text{For all $(\mathbb{M}, \sigma)$},~ \\ & \text{ ($\neg(\forall x. F)_{\mathbb{M}[\sigma]} = \texttt{true}$ and $(\exists x. (\neg F))_{\mathbb{M}[\sigma]} = \texttt{true}$) or $\neg(\forall x. F)_{\mathbb{M}[\sigma]} = \texttt{false}$} \\ \iff & \text{For all $(\mathbb{M}, \sigma)$},~ \\ & \text{ ($(\forall x. F)_{\mathbb{M}[\sigma]} = \texttt{false}$ and $(\exists x. (\neg F))_{\mathbb{M}[\sigma]} = \texttt{true}$) or $(\forall x. F)_{\mathbb{M}[\sigma]} = \texttt{true}$} \\ \iff & \text{For all $(\mathbb{M}, \sigma)$},~ \\ & \text{ (some $e \in M$ makes $F_{\mathbb{M}[\sigma[x:=e]]} = \texttt{false}$ and some $e \in M$ makes $\neg F_{\mathbb{M}[\sigma[x:=e]]} = \texttt{true}$)}\\ & \text{ or for all $e \in M$ there is $F_{\mathbb{M}[\sigma[x:=e]]} = \texttt{true}$} \\ \iff & \text{For all $(\mathbb{M}, \sigma)$},~ \\ & \text{ (some $e \in M$ makes $F_{\mathbb{M}[\sigma[x:=e]]} = \texttt{false}$ and some $e \in M$ makes $F_{\mathbb{M}[\sigma[x:=e]]} = \texttt{false}$)}\\ & \text{ or for all $e \in M$ there is $F_{\mathbb{M}[\sigma[x:=e]]} = \texttt{true}$} \\ \iff & \text{For all $(\mathbb{M}, \sigma)$},~ \text{some $e \in M$ makes $F_{\mathbb{M}[\sigma[x:=e]]} = \texttt{false}$} \\ & \text{ or for all $e \in M$ there is $F_{\mathbb{M}[\sigma[x:=e]]} = \texttt{true}$} \\ \iff & \text{For all $(\mathbb{M}, \sigma)$},~ \texttt{true} \\ \iff & \texttt{true} \end{aligned}$

证明的步骤就是不断地按照我们之前给出的定义展开符号，从而将目标语言完全转化为元语言，并在元语言层面得到一个永真的结果。这样的证明或许有些像废话——但意义确实需要一个元语言来描述，而且这种语言的转换本身就是非平凡的。如果读者对这样的解释仍然不满意，我们在下一节中会给出更形式化的语法证明。

Case 02

考虑自然数集导出的结构 $\mathcal{N} = (\mathbb{N}, I)$，证明该结构能满足：对于任意 $x$ 都存在 $y$ 使得 $x < y$ 成立：

$\begin{aligned} & \mathcal{N} \models \forall x. \exist y. x < y \\ \iff & \text{For all $\sigma$, } \mathcal{N} \models_{\sigma} \forall x. \exist y. x < y \\ \iff & \text{For all $\sigma$, } (\forall x. \exists y. x < y)_{\mathcal{N}[\sigma]} = \texttt{true} \\ \iff & \text{For all $\sigma$, } \text{for all $e_1 \in \mathbb{N}$, there is $(\exists y. x < y)_{\mathcal{N}[\sigma[x:=e_1]]} = \texttt{true}$} \\ \iff & \text{For all $\sigma$, } \text{for all $e_1 \in \mathbb{N}$, there is some $e_2 \in \mathbb{N}$ makes $(x < y)_{\mathcal{N}[\sigma[x:=e_1][y=e_2]]} = \texttt{true}$} \\ \iff & \text{For all $\sigma$, } \text{for all $e_1 \in \mathbb{N}$, there is some $e_2 \in \mathbb{N}$ makes $(e_1, e_2) \in I(<)$} \\ \iff & \text{For all $\sigma$, } \text{for all $e_1 \in \mathbb{N}$, there is $e_2=I(S)(e_1)$ makes $(e_1, e_2) \in I(<)$} \\ \iff & \text{For all $\sigma$, } \text{for all $e_1 \in \mathbb{N}$, \texttt{true}} \\ \iff & \text{For all $\sigma$, } \texttt{true} \\ \iff & \texttt{true} \end{aligned}$

这里我们在处理 for some 时，通过选取了结构论域中适当的元素带入完成了证明。其余的流程与上一个例子是几乎一致的。

---

语法可证

接下来我们考虑用另一种风格对符号的意义进行形式化，介绍如何在 Gentzen 推理系统（G 系统）中通过纯语法变换的形式进行证明。这一风格与上一节中的 $\lambda$-calculus 的形式化风格几乎一致——我们甚至需要定义一些相同的语法过程如下：

项的自由变元

$FV(T) = \begin{cases} \{v\} & T \equiv v \\ \emptyset & T \equiv c \\[3pt] \bigcup\limits_{i=1}^{\mu(f)} FV(t_i) & T \equiv f(T_1, \dots T_{\mu(f)}) \end{cases}$

这里 $v \in V, c \in \mathscr{L}_c, f \in \mathscr{L}_f$

项的替换

$T_1[T_2/x] = \begin{cases} T_2 & T_1 \equiv x \\ v & T_1 \equiv v \land v \not \equiv x \\ c & T_1 \equiv c \\ f(T_3[T_2/x], T_4[T_2/x]\dots) & T_1 \equiv f(T_3, T_4, \dots) \end{cases}$

注意这里要求 $x \in V$。

公式的自由变元

$FV(F) = \begin{cases} \bigcup\limits_{i = 1}^{\mu(P)} FV(T_i) & F \equiv P(T_1, \dots, T_{\mu(P)}) \\ FV(F') & F \equiv (\neg F') \\ FV(F_1) \cup FV(F_2) & F \equiv F_1 * F_2 \\ FV(F') - \{v\} & F \equiv Qv.F' \end{cases}$

这里 $P \in \mathscr{L}_P\cup\{\equiv\}, * \in \{\land, \lor, \to\}, Q \in \{\forall, \exist\}$

公式的替换

$F[T/x] = \begin{cases} P(T_1[T/x], \dots,T_{\mu(P)}[T/x]) & F \equiv P(T_1, \dots, T_{\mu(P)}) \\ (\neg F'[T/x]) & F \equiv (\neg F') \\ (F_1[T/x] * F_2[T/x]) & F \equiv F_1 * F_2 \\ Qx.F' & F \equiv Qx.F' \\ Qy.(F'[T/x]) & F \equiv Qy.F' \text{ and } y \not\in FV(T) \text{ and } y \not\equiv x \\ Qz.(F'[z/y][T/x]) & F \equiv Qy.F' \text{ and } y \in FV(T) \text{ and } y \not\equiv x \text{ and } z = \texttt{freshID}() \end{cases}$

注意量词的处理方式与我们在 $\lambda$-calculus 处理 $\lambda$ 的方式很相近。

接着正如我们在 $\lambda$-calculus 中定义推导一样，我们可以定义序贯(sequent) 如下：

$\Gamma \vdash \Delta$

这里 $\Gamma$ 和 $\Delta$ 都是公式的有穷集合，$\Gamma$ 称为前件、$\Delta$ 称为后件。实际上，像 $\lambda$-calculus 中的 $\to$ 与一阶谓词逻辑语言中的 $\vdash$ 这样的定义也被称为相继式演算(sequent calculus)。符号 $\vdash$ 也可以理解为「语法上可以导出」，其含义大概是：当 $\Gamma$ 中的每个公式都为真时，$\Delta$ 中至少有一个公式为真。按这样的理解，我们可以给出公理：

$\Gamma, F, \Delta \vdash \Lambda, F, \Theta$

该公理的含义是，当前件和后件中忽略位置关系有相同的公式 $F$ 出现时，这一步演算就是可行的。给定公理之后，我们就可以纯形式地给出一系列语法规则：

$\begin{aligned} \dfrac {\Gamma, \Delta \vdash \Lambda, F} {\Gamma, \neg F, \Delta \vdash \Lambda} \small\text{$\neg$L} \qquad&\qquad \dfrac {\Gamma, F \vdash \Lambda, \Theta} {\Gamma \vdash \Lambda, \neg F, \Theta} \small\text{$\neg$R} \\[6pt] \dfrac {\Gamma, F_1, \Delta \vdash \Lambda \qquad \Gamma, F_2, \Delta \vdash \Lambda} {\Gamma, F_1 \lor F_2, \Delta \vdash \Lambda} \small\text{$\lor$L} \qquad&\qquad \dfrac {\Gamma \vdash \Lambda, F_1, F_2, \Theta} {\Gamma \vdash \Lambda, F_1 \lor F_2, \Theta} \small\text{$\lor$R} \\[6pt] \dfrac {\Gamma, F_1, F_2, \Delta \vdash \Lambda} {\Gamma, F_1 \land F_2, \Delta \vdash \Lambda} \small\text{$\land$L} \qquad&\qquad \dfrac {\Gamma \vdash \Lambda, F_1, \Theta \qquad \Gamma \vdash \Lambda, F_2, \Theta} {\Gamma \vdash \Lambda, F_1 \land F_2, \Theta} \small\text{$\land$R} \\[6pt] \dfrac {\Gamma, \Delta \vdash F_1, \Lambda \qquad \Gamma, F_2, \Delta \vdash \Lambda} {\Gamma, F_1 \to F_2, \Delta \vdash \Lambda} \small\text{$\to$L} \qquad&\qquad \dfrac {\Gamma, F_1 \vdash \Lambda, F_2, \Theta} {\Gamma \vdash \Lambda, F_1 \to F_2, \Theta} \small\text{$\to$R} \\[6pt] \dfrac {\Gamma, F[T/x], \forall x.F, \Delta \vdash \Lambda} {\Gamma, \forall x.F, \Delta \vdash \Lambda} \small\text{$\forall$L} \qquad&\qquad \dfrac {\Gamma \vdash \Lambda, F[y/x], \Theta} {\Gamma \vdash \Lambda, \forall x. F, \Theta} \small\text{$\forall$R} \\[6pt] \dfrac {\Gamma, F[y/x], \Delta \vdash \Lambda} {\Gamma, \exists x.F, \Delta \vdash \Lambda} \small\text{$\exists$L} \qquad&\qquad \dfrac {\Gamma \vdash \Lambda, F[T/x], \exists x. F, \Theta} {\Gamma \vdash \Lambda, \exists x. F, \Theta} \small\text{$\exists$R} \\[6pt] \end{aligned}$

这里横线最左侧是规则的名称，$y$ 是新变元，$T$ 是可以随意引入的项。可以发现这些规则刻画了最关切的符号（逻辑连接词、量词）分别出现在 $\vdash$ 左右时的推理方式。通过使用这些规则，我们实际上可以画出一棵证明树。

考虑两个例子：

• 对于式 $\neg(\forall x. F) \to \exists x. (\neg F)$，应用规则的序列可以是：

  

• 对于式 $(\exists x. P(x) \to \forall y.Q(y)) \to \forall z. (P(z) \to Q(z))$，应用规则的序列可以是：

  

可以发现，我们通过这种树形图组织起一些语法规则，而在树的最顶层得到了一些公理。这意味着我们可以从这些公理出发，按照图中规定的顺序从上到下、从左到右地应用语法规则，就可以演算出最下方的序贯。如果存在这样的一棵证明树，我们就称最下方的序贯是可证的(provable)。

前面提到语义可满足、语法可证这两个定义都是用于形式化一阶谓词逻辑语言的途径，尽管他们看起来完全不同。接下来我们将说明这两种方式的等价性。

序贯 $\Gamma$ 为 $A_1, A_2, \dots A_n$，而序贯 $\Delta$ 为 $B_1, B_2, \dots, B_m$，引入记号 $\Gamma \models \Delta$ 表示序贯 $\Gamma \vdash \Delta$ 有效，即

$\models \big(\bigwedge_{i=1}^{n} A_i \big) \to \big(\bigvee_{i=1}^{m} B_i\big)$

而接下来我们将证明 G 系统的两个关键性质：

• Soundness: $\Gamma \vdash \Delta \implies \Gamma \models \Delta$

  即若 $\Gamma \vdash \Delta$ 可证，则 $\Gamma \models \Delta$

• Completeness: $\Gamma \vdash \Delta \iff \Gamma \models \Delta$

  即 $\Gamma \vdash \Delta$ 可证与 $\Gamma \models \Delta$ 等价

Soundness

这一证明只需使用结构归纳法。

• Base: 若 $\Gamma \vdash \Delta$ 为公理，则 $\Gamma \models \Delta$。

  证明假设 $A_i \equiv B_j$，接着按语义方法将目标语言转化成元语言易见。

• Induction: 对 $\Gamma \vdash \Delta$ 证明树中应用规则的层数归纳即可。

  想要完成归纳步骤，我们只需对每条规则证明上方序贯有效等价于下方序贯有效。

  如对于规则 $\land R$，我们按语义方法将句子

  $({\Gamma \models \Lambda, F_1, \Theta \texttt{ and } \Gamma \models \Lambda, F_2, \Theta}) \iff ({\Gamma \models \Lambda, F_1 \land F_2, \Theta})$

  完全展开成元语言即容见。

Completeness

• $\Rightarrow$: 即 Soundness

• $\Leftarrow$: 考虑先证明 $\Delta$ 是单个公式 $F$ 的情形。

  我们设 $\Gamma \models F$，讨论 $\Gamma$ 的性质。

  • 若存在 $\Gamma$ 的有穷子集 $\Lambda$ 使得 $\Lambda \vdash$ 可证（称 $\Gamma$ 是矛盾的）：

    此时有 $\Gamma \vdash$ 可证。只需在 $\Lambda \vdash$ 的证明树中涉及的所有序贯的前件中添加 $\Gamma \setminus \Lambda$ 即可。

    那么自然地又有 $\Gamma \vdash F$ 可证，只需在 $\Gamma \vdash$ 的证明树中涉及的所有序贯的后件中添加 $F$ 即可。

    注意到进行这种添加后，最上方的公理仍然是公理，而所有规则也都仍可应用。于是我们证明了存在一棵 $\Gamma \vdash F$ 的证明树，即它是可证的。

  • 若 $\Gamma$ 中不存在这样的有穷子集（称 $\Gamma$ 是协调的）：

    考虑反证法，假设 $\Gamma \vdash F$ 不可证，

    于是我们知道 $\Gamma, \neg F \vdash$ 不可证，否则应用 $\neg L$ 就能得到 $\Gamma \vdash F$ 可证，与假设矛盾。

    此时我们知道 $\Gamma, \neg F$ 是协调的。而对于协调的公式集，我们可以构造出对应的 Hinkin 集并证明该集合实际上又是一个 Hintikka 集，而后者总是可满足的。这部分的证明我们由于篇幅限制姑且略去。其要义大概是规定集合的结构与特殊性质，随后按结构归纳法完成证明。

    总之我们知道 $\Gamma, \neg F$ 是可满足的，即存在模型 $\mathcal{M}$ 与赋值 $\sigma$ 使 $\mathcal M \models_\sigma \Gamma, \neg F$。设 $\Gamma$ 为 $A_1, \dots A_n$，也就是有 $\mathcal M \models_\sigma \bigwedge_{i=1}^{n} A_i$ 与 $\mathcal M \models_\sigma \neg F$ 均成立。又由于 $\Gamma \models F$，所以同样有 $\mathcal{M} \models_\sigma (\bigwedge_{i=1}^{n} A_i) \to F$，矛盾。故知假设不成立，$\Gamma \vdash F$ 可证。

由此，我们证明了纯形式的 G 系统与一阶谓词逻辑语言的语义之间存在被我们称作 Completeness 的等价性。这也意味着至少对于一阶谓词逻辑而言，我们有了一种机械的、形式的手段去认识它的意义。毫不夸张地说，这件事「见证了人类理性的伟大」，我们在克服语言的不确定性、克服逻辑的不严密性上跨出了伟大的一步。

但是宋方敏老师的话还有后半句，「数理逻辑见证了人类理性的无助」。我们接下来通过介绍哥德尔的不完备性定理，再一次展示人类面对真理、面对科学问题时的无助：我们唯一知道的就是，我们无法知道。

---

Chomskyan School

• Belief in Universal Grammar and generative grammar
• the context-free languages and the Chomsky hierarchy
• The rise and fail of Behaviorism

On the way…

Type Theory

• Simply Typed Lambda Calculus
• Curry-Howard Isomorphism
• Proof Assistance

On the way…

Programming Languages

• Context-free Grammar, again
• Operational, Denotational and Axiomatic Formal Semantics
• Reasoning about programs

On the way…